cho tam giác ABC cân tại A . kẻ tia phân giác BD ,lấy G là trung điểm của BC
a, chứng minh AG là tia phân giác của BAC
b, Gọi H là giao điểm của AGvà BD. chứng minh CH là tia p-hân giác của tam giác ABC
Quảng cáo
1 câu trả lời 124
a) Chứng minh AG là phân giác của góc $\angle BAC$
Giả thiết:
Tam giác ABC cân tại A ⇒ $AB = AC$
G là trung điểm của $BC$ ⇒ $BG = GC$
Xét hai tam giác $\triangle ABG$ và $\triangle ACG$:
$AB = AC$ (giả thiết tam giác cân)
$AG$ là cạnh chung
$BG = GC$ (G là trung điểm BC)
→ Theo trường hợp cạnh – cạnh – cạnh (c.c.c), ta có:
\triangle ABG \cong \triangle ACG
⇒ $\angle BAG = \angle CAG$
→ AG là phân giác của góc $\angle BAC$ (đpcm)
b) Gọi H là giao điểm của AG và BD, chứng minh CH là phân giác của tam giác ABC
Xét tam giác ABC câ
⇒ Góc $\angle ABC = \angle ACB$ (vì hai đáy bằng nhau)
Ta có:
BD là phân giác của $\angle ABC$
AG là phân giác của $\angle BAC$
G là trung điểm của $BC$
⇒ H là giao điểm của hai phân giác → trung tâm nội tiếp tam giác ABC
Do H là giao điểm các phân giác trong → H nằm trên phân giác góc C
⇒ CH là phân giác của góc $\angle ACB$ (đpcm)
a) $AG$ là phân giác của $\angle BAC$
b) $CH$ là phân giác của $\angle ACB$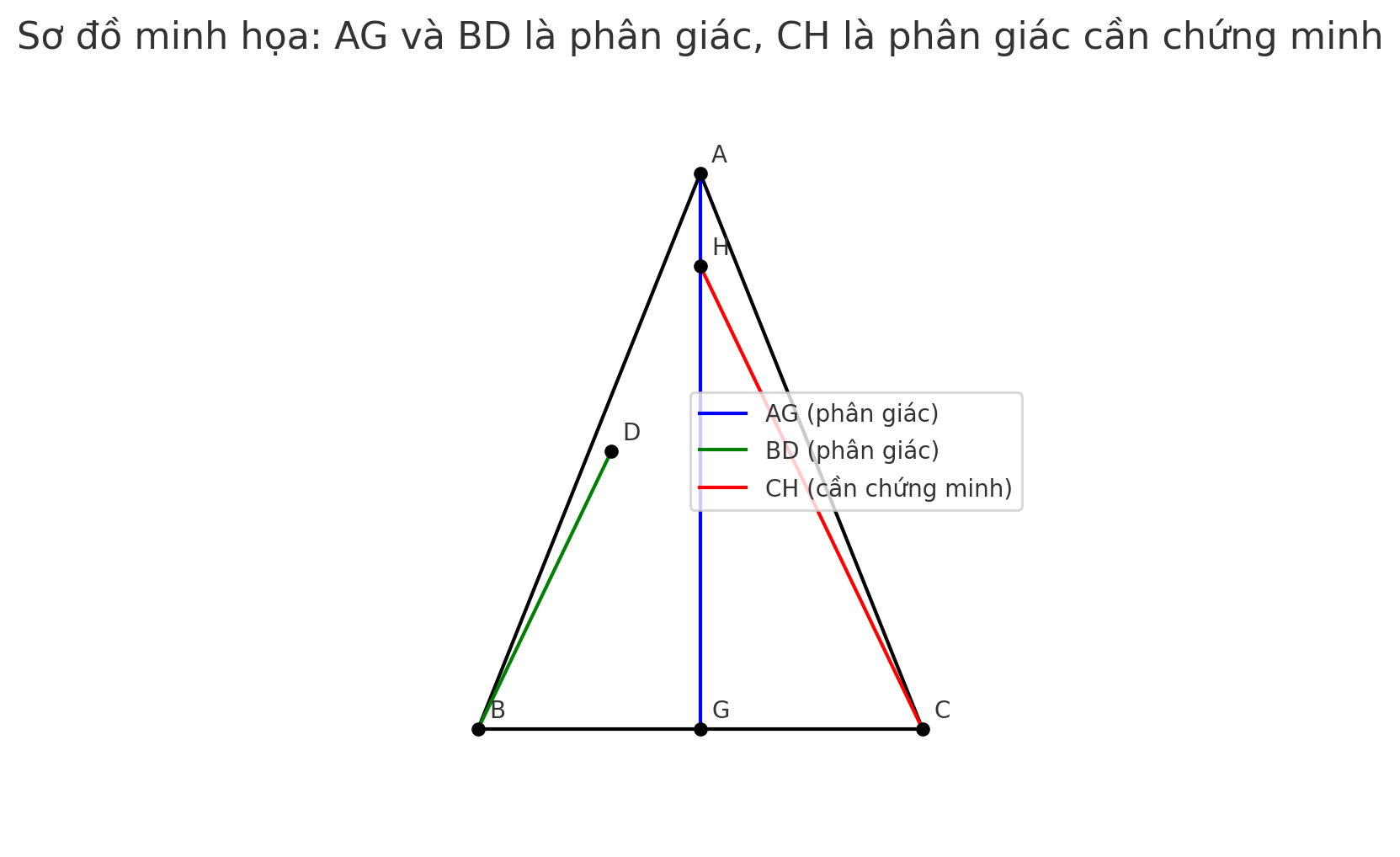
Quảng cáo
Bạn hỏi - Chuyên gia trả lời
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Đã trả lời bởi chuyên gia
7808 -
Đã trả lời bởi chuyên gia
7313
-
Đã trả lời bởi chuyên gia
6304
-
보고 싶어요
2140 điểm
-
😗
900 điểm
-
🌷김은✨
590 điểm
-
`color{blue}text{HuyTùng☢`
575 điểm
-
𝘳𝘺𝘯.𝘭𝘦𝘦ッ
540 điểm
-
jgdmaX
345 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
300 điểm
-
Kiều Anh 295 điểm
-
돈이없다 💸😭
260 điểm
-
༘⋆nhỏ nho𓏲ּ𝄢
225 điểm
-
devestro
210 điểm
-
너 없는 파리
190 điểm
-
Ben 23K
180 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
160 điểm
-
Hai Trieu
150 điểm
Rút gọn
Bài viết mới nhất Lớp 7
-
2 năm trước4947
