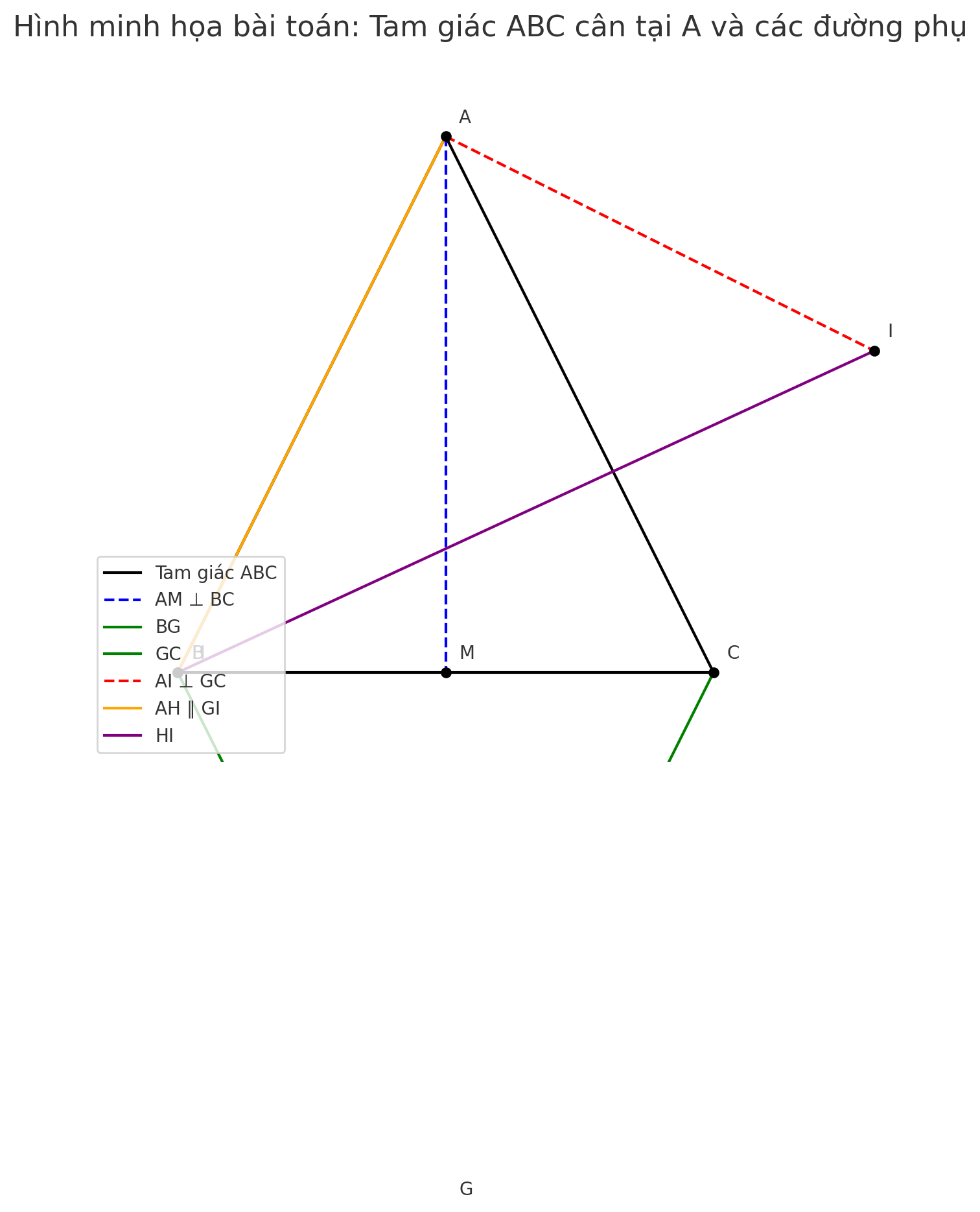
tam giác ABC cân tại A (Â &lt; 90°). Kẻ AM vuông góc với BC tạiM. a) Chứng minh:...

· 20:42 13/05/2025

Đề kiểm tra Học kì 2 Toán 7

tam giác ABC cân tại A (Â < 90°). Kẻ AM vuông góc với BC tại
M. a) Chứng minh: A ABM = A ACM, từ đó chứng minh M là trung
điểm của BC.
b) Trên tia đối của tia MA lấy điểm G sao cho MB = MG. Chứng minh: BG 1 GC.
c) Qua A vẽ đường thẳng vuông góc với tia GC, đường thẳng đó cắt tia GC tại I. So sánh độ dài GI và AC
d) Qua A vẽ đường thẳng song song với GI, cắt tia GB tại H.
Chứng minh: HI // BC.

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

3 câu trả lời 166

Sang Phạm

7 tháng trước

a) Chứng minh $\triangle ABM = \triangle ACM$

Ta có:

$AB = AC$ (tam giác cân tại A)
$AM$ chung
$\angle AMB = \angle AMC = 90^\circ$ (vì AM ⊥ BC)

⇒ $\triangle ABM = \triangle ACM$ (theo trường hợp cạnh – huyền – góc vuông)

Suy ra: BM = MC
⇒ M là trung điểm của BC (đpcm)

b) Trên tia đối của tia MA lấy G sao cho MB = MG. Chứng minh BG ⊥ GC

Ta có:

MB = MG (giả thiết)
M là trung điểm của BC (từ câu a)
G nằm trên tia đối của MA nên G – M – A thẳng hàng.

Xét tam giác BGC:

BM = MG
MC = MB ⇒ MG = MC
⇒ G là đối xứng của B qua M và đối xứng của C qua M
⇒ Tam giác BGC cân tại G và có $\angle BGC = 90^\circ$
→ BG ⊥ GC (đpcm)

c) Qua A vẽ đường thẳng ⊥ GC, cắt tia GC tại I. So sánh GI và AC

Ta có:

$\angle AIG = 90^\circ$ (do AI ⊥ GC)
Tam giác ACG cân tại A (vì AB = AC và G đối xứng với B qua M)

Xét tam giác vuôn AIG vuông tại I
→ I là chân đường vuông góc từ A xuống GC
⇒ GI là hình chiếu của đoạn AC lên GC

→ Theo định lý hình chiếu:

$< b r / > G I < A C < b r / >$
GI < AC

$GI < AC$ (vì hình chiếu luôn ngắn hơn đoạn xiên trừ khi vuông góc – mà ở đây không vuông góc)

d) Qua A vẽ đường thẳng song song với GI, cắt tia GB tại H. Chứng minh: HI // BC

Ta có: $AH \parallel GI$, mà GI ⊥ GC (từ câu c)
→ $AH \perp GC$

Xét tam giác BGC, ta có:

$BG \perp GC$ (từ câu b)
AH ⊥ GC → HI ⊥ GC (vì cùng thuộc đường thẳng qua A song song GI)

⇒ HI ⊥ GC, mà BC cũng ⊥ AM và nằm trên đường thẳng vuông góc với AM

Mà $M \in BC$, GC đối xứng với BC qua M ⇒ HI // BC (đpcm)

a) $\triangle ABM = \triangle ACM$, ⇒ M là trung điểm của BC
b) MB = MG ⇒ BG ⊥ GC
c) Qua A vẽ ⊥ GC, cắt GC tại I ⇒ $GI < AC$
d) Qua A vẽ đường song song GI cắt GB tại H ⇒ $HI // BC$