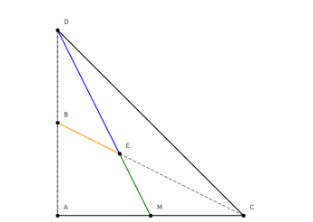
a, so sánh góc D với góc A
b, gọi B là trung điểm của AD , lấy điểm E trên CB sao cho BE = 1/3 BC. Chứng minh ba điểm DE và M ( M là trung điểm của CA ) thẳng hàng
Quảng cáo
2 câu trả lời 238
a) So sánh góc D và góc A
Trong tam giác $\triangle ACD$:
$CA < CD$ ⇒ cạnh đối diện với góc D là CA nhỏ hơn cạnh đối diện với góc A là CD
Cạnh đối diện nhỏ hơn thì góc đối cũng nhỏ hơn
⟹ $\angle D < \angle A$ (Đáp án)
b) Chứng minh ba điểm D, E, M thẳng hàng
Ý tưởng: Sử dụng tỉ số chia đoạn và hệ thức trung điểm, sau đó áp dụng định lý Thales đảo hoặc đồng dạng, hoặc tọa độ hóa
Gọi $A = (0, 0)$, $C = (2a, 0)$, thì M = trung điểm CA ⇒ M = (a, 0)
Gọi $D = (0, 2b)$, ⇒ $B = \text{trung điểm AD} = (0, b)$
Đoạn CB nối từ $C = (2a, 0)$ đến $B = (0, b)$
Tìm tọa độ điểm E sao cho $BE = \frac{1}{3} BC$
Vector BC: từ B đến C là $\vec{BC} = (2a - 0, 0 - b) = (2a, -b)$
$\vec{BE} = \frac{1}{3} \vec{BC} = \left( \frac{2a}{3}, -\frac{b}{3} \right)$
⟹ Tọa độ điểm E là:
Kiểm tra xem 3 điểm D, E, M có thẳng hàng không
D = (0, 2b), E = $\left( \frac{2a}{3},\ \frac{2b}{3} \right)$, M = (a, 0)
Gọi 3 điểm thẳng hàng nếu các vector DE và EM cùng phương:
Tính vector:
$\vec{DE} = E - D = \left( \frac{2a}{3} - 0,\ \frac{2b}{3} - 2b \right) = \left( \frac{2a}{3},\ -\frac{4b}{3} \right)$
$\vec{EM} = M - E = \left( a - \frac{2a}{3},\ 0 - \frac{2b}{3} \right) = \left( \frac{a}{3},\ -\frac{2b}{3} \right)$
Ta có:
→ Hai vector cùng phương ⇒ 3 điểm D, E, M thẳng hàng (đpcm)
a) $\angle D < \angle A$
b) D, E, M thẳng hàng
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


