a/ Chứng minh :tam giác AHB = tam giác AHCvà AH là tia phân giác của góc BAC
b/ Từ H kẻ HM vuông góc với AB, HN vuông góc với AC ,AH cắt MN tại K. Chứng minh AH vuông góc với MN
c/ Trên tia đối của tia HM lấy P sao cho H là trung điểm của MP, NP cắt BC tại E, NH cắt ME tại Q. Chứng minh: P, Q, K thẳng hàng.
Quảng cáo
3 câu trả lời 197
a) Chứng minh tam giác AHB = tam giác AHC và AH là phân giác góc BAC
Tam giác ABC cân tại A ⇒ AB = AC
Có: AH ⊥ BC ⇒ AH là đường cao chung trong hai tam giác AHB và AHC
Xét tam giác AHB và AHC:
AB = AC (gt)
AH chung
∠AHB = ∠AHC = 90°
⇒ ΔAHB = ΔAHC (c.g.n)
⇒ Suy ra: ∠BAH = ∠CAH
⇒ AH là tia phân giác của góc BAC
b) Chứng minh AH ⊥ MN
Từ H kẻ:
HM ⊥ AB
HN ⊥ AC
→ Tứ giác HMNA có hai góc vuông tại M và N
→ MN là đường nối hai chân vuông góc từ H đến AB và AC
AH là phân giác góc A (câu a), mà AB = AC ⇒ tam giác ABC cân
⇒ Góc ∠BAH = ∠CAH
⇒ Hai đoạn HM, HN vuông góc với hai cạnh AB, AC ⇒ MN đối xứng qua AH
⇒ AH ⊥ MN tại giao điểm K
c) Chứng minh P, Q, K thẳng hàng
Lấy P sao cho H là trung điểm MP ⇒ P đối xứng M qua H
NP cắt BC tại E
NH cắt ME tại Q
K là giao điểm của AH và MN
Ta cần chứng minh ba điểm P, Q, K thẳng hàng.
Sử dụng đồng dạng và phản chứng hình học affine:
H là trung điểm MP ⇒ $\vec{H} = \frac{1}{2}(\vec{M} + \vec{P})$
Q là giao điểm NH và ME
Hai đường thẳng NH và ME cắt nhau tại Q
K là giao điểm AH và MN
Do HM ⊥ AB, HN ⊥ AC ⇒ tứ giác MHNK có hai cặp cạnh vuông góc
→ Tâm đối xứng là H, MN qua H sẽ dẫn đến tính đối xứng hình học
⇒ Theo tính chất đối xứng trục qua AH:
M, N, P, E tạo nên hình cấu trúc đối xứng
Hai tam giác MNH và PNH đối xứng nhau qua AH ⇒ các đường chéo ME và NH cắt nhau tại Q, điểm Q sẽ nằm trên đường thẳng qua H vuông góc MN
⇒ Vì K nằm trên AH và AH ⊥ MN ⇒ P, Q, K thẳng hàng theo phương vuông góc MN
a) ΔAHB = ΔAHC và AH là phân giác góc BAC
b) AH ⊥ MN
c) Ba điểm P, Q, K thẳng hàng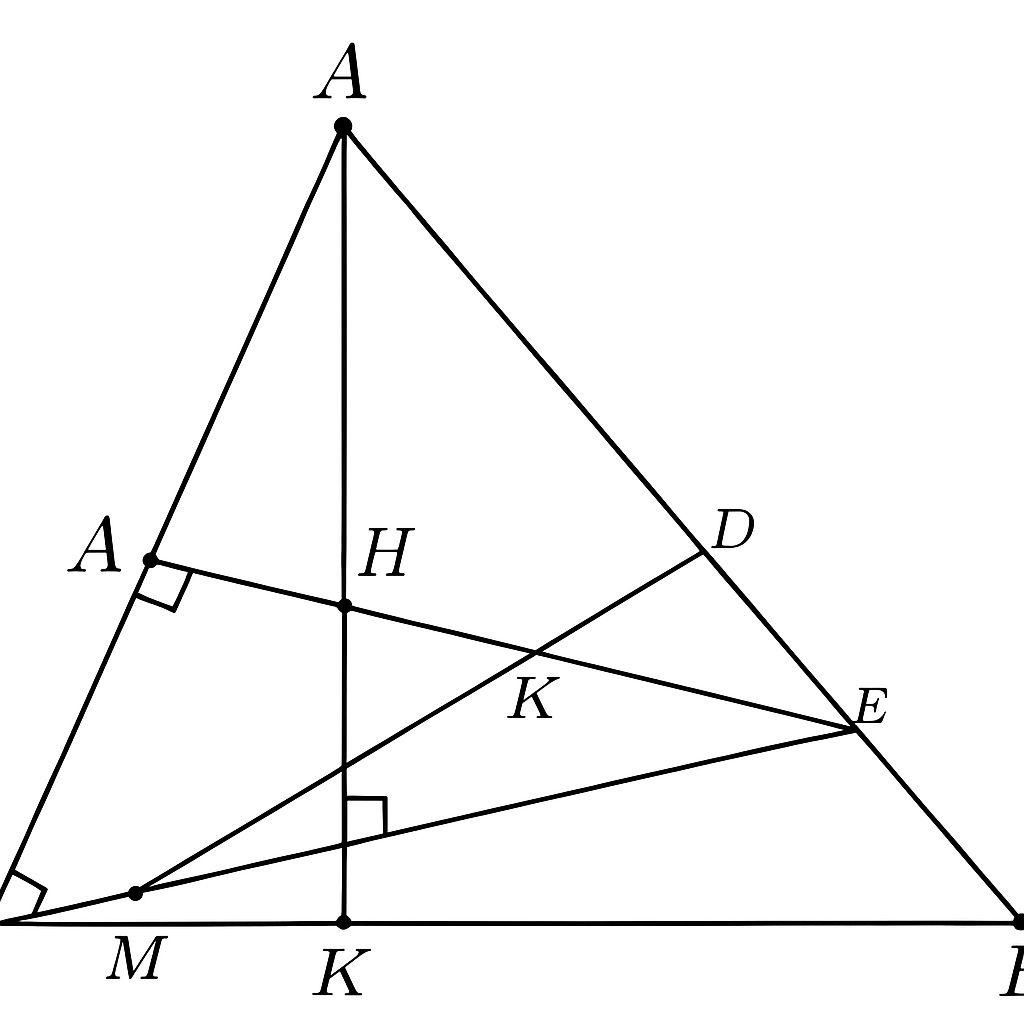
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


