A, chứng minh AB bằng B H
B, chứng minh AK bằng H C. Từ đó suy ra B K C cân tại B
Quảng cáo
3 câu trả lời 136
a) Chứng minh $AB = BH$
Tam giác $ABC$ vuông tại A ⇒ ∠CAB = 90°
BD là phân giác ⇒ D ∈ AC
Qua D, kẻ $DH \perp BC$ tại H, cắt AB tại K.
Xét hai tam giác vuông ABH và HBD:
∠ABH = 90° (do tam giác ABC vuông tại A)
$DH \perp BC$ ⇒ ∠DHB = 90°
Xét hai tam giác vuông ABH và HBK:
Có ∠ABH = ∠HBK = 90°
Có góc ∠H chung
BD là phân giác =>
Mặt khác, do ∠CAB = 90°, nên hai tam giác ABH và HBK đều vuông và có chung cạnh góc vuông là BH
⇒ Xét tam giác ABH và tam giác HBD:
Góc B chung
Hai góc vuông tại A và H
⇒ ΔABH = ΔHBK (cạnh huyền và góc nhọn)
⇒ AB = BH
b) Chứng minh $AK = HC$
Xét hai tam giác vuông AKD và DHC:
∠AKD = ∠DHC = 90° (do DH ⊥ BC, DH ⊥ AK)
Có D chung
BD là phân giác ⇒
Do AB = BH (theo câu a), mà AB nằm trên cạnh vuông của tam giác vuông ⇒ suy ra AK = HC
⇒ AK = HC
Tam giác $BKC$ có:
AB = BH ⇒ BK = BK (chung)
AK = HC ⇒ hai đoạn thẳng từ K đến hai cạnh bằng nhau
⇒ Tam giác $BKC$ cân tại B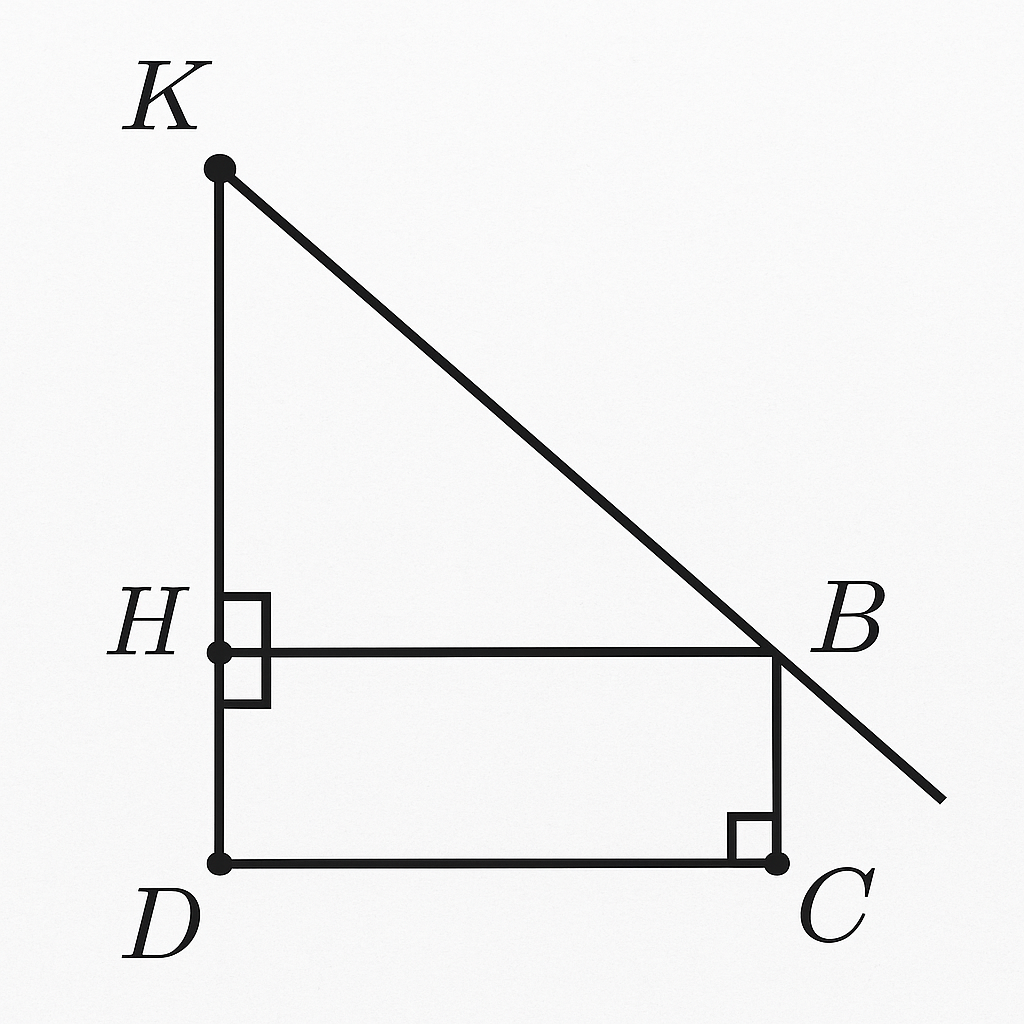
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669



