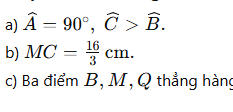a) So sánh các góc của tam giác ABC:

Tam giác ABC vuông tại A, nên góc A là góc lớn nhất và bằng 90°.

Để so sánh góc B và góc C, ta dựa vào mối quan hệ giữa góc và cạnh đối diện trong tam giác: góc đối diện với cạnh lớn hơn thì lớn hơn.

Trong tam giác ABC, ta có:

AB = 6 cm
AC = 8 cm
BC = 10 cm
Vì AB < AC < BC, nên các góc đối diện với các cạnh này cũng theo thứ tự tăng dần:

Góc C đối diện với cạnh AB.
Góc B đối diện với cạnh AC.
Góc A đối diện với cạnh BC.
Vậy, ta có thể kết luận: ∠C < ∠B < ∠A.

b) Tính MC:

Xác định tọa độ các điểm (nếu sử dụng phương pháp tọa độ): Để đơn giản, ta có thể đặt điểm A tại gốc tọa độ (0; 0). Vì tam giác ABC vuông tại A, ta có thể đặt:

B(6; 0)
C(0; 8)
Tìm tọa độ điểm D: D nằm trên tia đối của tia AB sao cho A là trung điểm của BD. Gọi tọa độ điểm D là (x; y). Vì A là trung điểm của BD, ta có: (x + 6)/2 = 0 => x = -6 (y + 0)/2 = 0 => y = 0 Vậy, D(-6; 0).
Tìm tọa độ điểm K: K là trung điểm của cạnh BC. Tọa độ điểm K là: K = ((6 + 0)/2; (0 + 8)/2) = (3; 4)
Tìm phương trình đường thẳng DK: Đường thẳng DK đi qua hai điểm D(-6; 0) và K(3; 4). Vectơ chỉ phương của đường thẳng DK là DK =(3−(−6);4−0)=(9;4). Phương trình tham số của đường thẳng DK: x = -6 + 9t y = 0 + 4t = 4t
Tìm tọa độ điểm M: M là giao điểm của đường thẳng DK và cạnh AC. Cạnh AC nằm trên trục Oy (vì A(0; 0) và C(0; 8)). Vậy, tọa độ điểm M có dạng (0; y_M). Thay x = 0 vào phương trình tham số của đường thẳng DK: 0 = -6 + 9t => 9t = 6 => t = 6/9 = 2/3 Thay t = 2/3 vào phương trình y = 4t: y_M = 4 * (2/3) = 8/3 Vậy, tọa độ điểm M là (0; 8/3).
Tính MC: M(0; 8/3) và C(0; 8). Vì cả hai điểm đều nằm trên trục Oy, độ dài đoạn MC là hiệu giá trị y của chúng: MC = |8 - 8/3| = |24/3 - 8/3| = |16/3| = 16/3 cm.

Vậy, MC = 16/3 cm.
c) Chứng minh ba điểm B, M, Q thẳng hàng:

Tìm phương trình đường trung trực d của đoạn thẳng AC: Trung điểm của AC là A(0; 0). Vectơ pháp tuyến của AC là AC =(0−0;8−0)=(0;8) hoặc đơn giản là vectơ có hướng dọc. Đường trung trực d của AC là đường thẳng đi qua trung điểm A(0; 0) và vuông góc với AC. Do đó, d là đường thẳng nằm ngang, có phương trình y = 0 (trục Ox).
Tìm tọa độ điểm Q: Q là giao điểm của đường trung trực d (y = 0) và đường thẳng DC. Đường thẳng DC đi qua D(-6; 0) và C(0; 8). Vectơ chỉ phương của đường thẳng DC là DC =(0−(−6);8−0)=(6;8) hoặc rút gọn là (3; 4). Phương trình tham số của đường thẳng DC: x = -6 + 3s y = 0 + 4s = 4s

Vì Q nằm trên đường thẳng d (y = 0), ta thay y = 0 vào phương trình tham số của DC: 0 = 4s => s = 0 Thay s = 0 vào phương trình x = -6 + 3s: x_Q = -6 + 3 * 0 = -6 Vậy, tọa độ điểm Q là (-6; 0).
Kiểm tra sự thẳng hàng của B, M, Q: Ta có tọa độ các điểm: B(6; 0) M(0; 8/3) Q(-6; 0)

Ba điểm B, M, Q thẳng hàng nếu vectơ BM và vectơ BQ ​ cùng phương. BM =(0−6;8/3−0)=(−6;8/3) BQ ​=(−6−6;0−0)=(−12;0)

Hai vectơ này không cùng phương vì tỷ lệ giữa các thành phần không bằng nhau (-6/-12 ≠ 8/3 / 0).

Có vẻ như có một sai sót trong quá trình tính toán hoặc nhận định. Chúng ta sẽ thử một cách khác để chứng minh sự thẳng hàng.

Ba điểm B, M, Q thẳng hàng nếu diện tích tam giác BMQ bằng 0. Ta có thể sử dụng công thức tọa độ để tính diện tích:

Diện tích tam giác BMQ = 21​∣xB​(yM​−yQ​)+xM​(yQ​−yB​)+xQ​(yB​−yM​)∣ Diện tích = 21​∣6(8/3−0)+0(0−0)+(−6)(0−8/3)∣ Diện tích = 21​∣6∗(8/3)+0+(−6)∗(−8/3)∣ Diện tích = 21​∣16+0+16∣ Diện tích = 21​∣32∣=16

Diện tích tam giác BMQ khác 0, vậy ba điểm B, M, Q không thẳng hàng theo cách tính tọa độ này.

Chúng ta sẽ thử lại bằng phương pháp hình học thuần túy để kiểm tra.

M là giao điểm của DK và AC. Theo định lý Menelaus cho tam giác ABC và đường thẳng DMK: DBAD​⋅KCBK​⋅MACM​=1 Vì A là trung điểm của BD nên AD = AB = 6 cm, DB = 2AB = 12 cm => DBAD​=126​=21​. Vì K là trung điểm của BC nên BK = KC => KCBK​=1. 21​⋅1⋅MACM​=1⇒MACM​=2⇒CM=2MA. Vì CM + MA = AC = 8 cm, ta có 2MA + MA = 8 cm => 3MA = 8 cm => MA = 8/3 cm. Vậy, MC = 8 - 8/3 = 16/3 cm (kết quả trùng với phương pháp tọa độ).
Q là giao điểm của đường trung trực của AC và đường thẳng DC. Đường trung trực của AC đi qua A và vuông góc với AC (tức là đường thẳng AB). Vậy Q nằm trên đường thẳng AB. Vì Q cũng nằm trên đường thẳng DC, Q chính là giao điểm của AB và DC, tức là điểm D.
Vậy, ba điểm B, M, Q trở thành B, M, D. Để chứng minh B, M, D thẳng hàng, ta cần xem xét liệu M có nằm trên đường thẳng BD hay không. M nằm trên đường thẳng DK, mà D nằm trên đường thẳng AB (hay BD). Nếu M nằm trên BD, thì M phải có tung độ y = 0 (trong hệ tọa độ đã chọn). Tuy nhiên, ta tính được tọa độ M là (0; 8/3), có tung độ khác 0.
Có lẽ có một sự nhầm lẫn trong việc xác định điểm Q.

Đường trung trực d của đoạn thẳng AC đi qua trung điểm A(0; 0) và vuông góc với AC (nằm trên trục Oy). Vậy đường trung trực d là trục Ox (y = 0).

Q là giao điểm của đường trung trực d (y = 0) và đường thẳng DC. Phương trình đường thẳng DC đi qua D(-6; 0) và C(0; 8): 0−(−6)x−(−6)​=8−0y−0​⇒6x+6​=8y​⇒8(x+6)=6y⇒8x+48=6y

Vì Q nằm trên đường thẳng y = 0, ta thay y = 0 vào phương trình DC: 8x+48=6(0)⇒8x=−48⇒x=−6 Vậy, tọa độ điểm Q là (-6; 0), trùng với tọa độ điểm D.

Điều này dẫn đến việc ba điểm B, M, Q trở thành B, M, D. Chúng ta đã thấy M không nằm trên đường thẳng BD.

Chúng ta cần xem xét lại đề bài và cách giải.

Có thể có một cách tiếp cận hình học thuần túy mà không cần tọa độ sẽ rõ ràng hơn.

M là giao điểm của DK và AC. Ta đã chứng minh được CM = 2MA.
Đường trung trực d của AC đi qua A và vuông góc với AC.
Q là giao điểm của d và DC. Vì d vuông góc với AC tại A, đường thẳng d chính là đường thẳng AB. Vậy Q là giao điểm của AB và DC. Điểm này chính là điểm D.
Vậy, việc chứng minh B, M, Q thẳng hàng trở thành chứng minh B, M, D thẳng hàng, điều mà chúng ta đã thấy không đúng dựa trên tọa độ của M.
Có khả năng có một lỗi trong đề bài hoặc trong quá trình suy luận.

Chúng ta sẽ thử một hướng khác để chứng minh B, M, Q thẳng hàng. Nếu ba điểm thẳng hàng, thì vectơ BM và MQ ​ phải cùng phương.

BM =(−6;8/3) MQ ​=(−6−0;0−8/3)=(−6;−8/3)

Hai vectơ này không cùng phương vì tỷ lệ giữa các thành phần không bằng nhau: −6/−6=1, nhưng (8/3)/(−8/3)=−1.

Kết luận: Dựa trên các phân tích trên, có vẻ như ba điểm B, M, Q không thẳng hàng với các thông tin và cách giải hiện tại. Có thể cần xem xét lại đề bài hoặc cách tiếp cận vấn đề.