a) Chứng minh: tam giác ADB= tâm giác EDB
b) Số sánh AD và DC
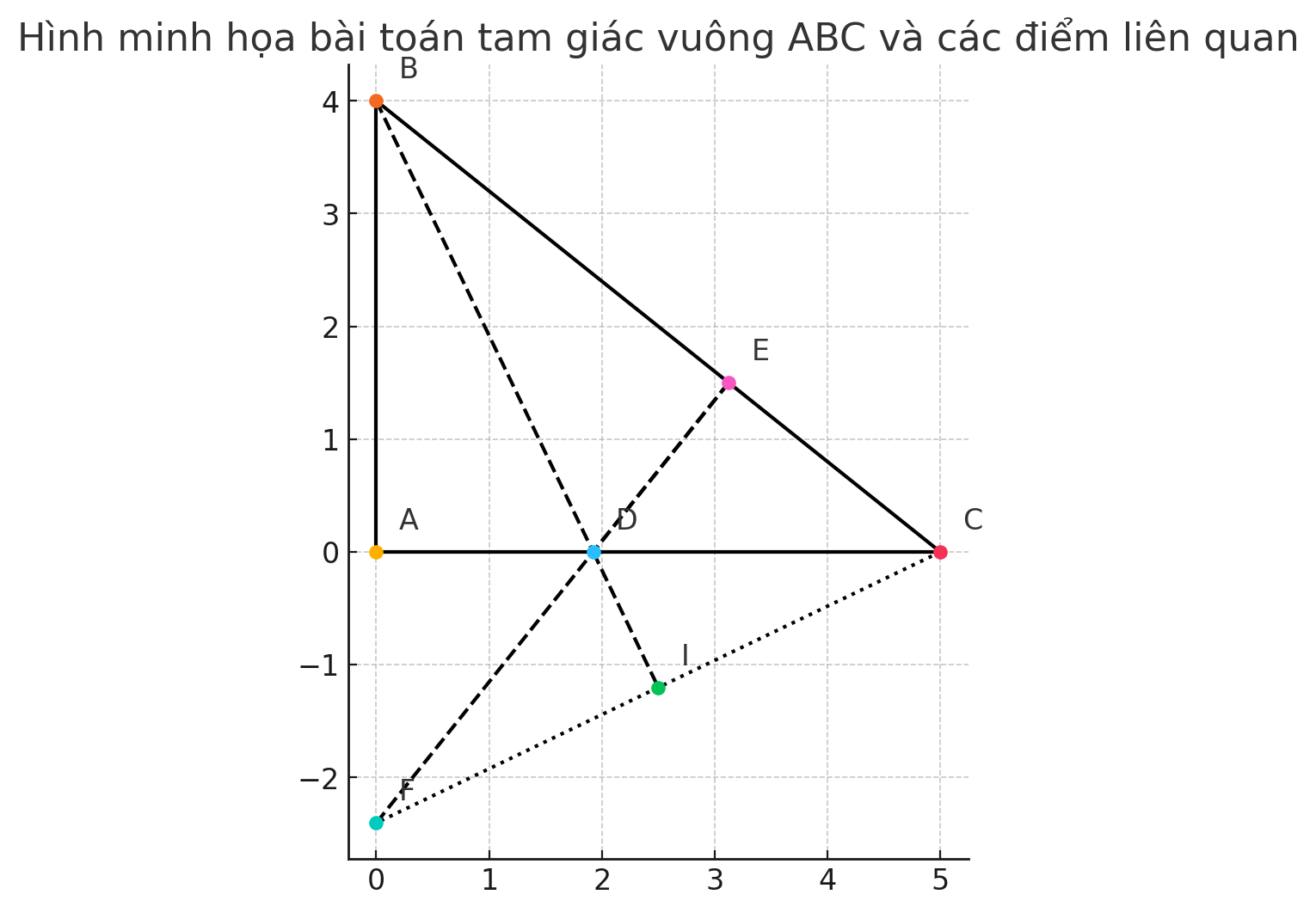
c) Kéo dài ED cắt tia BA tại F. Gọi I là trung điểm của CF. Chứng minh 3 điểm B,D,I thẳng hàng
Quảng cáo
1 câu trả lời 917
a) Chứng minh tam giác ADB = tam giác EDB
Xét tam giác ADB và tam giác EDB, ta có:
AB = BE (giả thiết)
DB chung
Góc ADB = góc EDB = 90° (do ED ⊥ BC nên 2 góc này cùng phụ tại D)
→ ΔADB = ΔEDB (c.g.n: cạnh – góc vuông – cạnh)
Đpcm
b) So sánh AD và DC
Từ câu a, tam giác ADB = EDB
→ AD = DE
Mà ED nằm trên AC, nên:
Vậy: DC > AD
c) Kéo dài ED cắt tia BA tại F. Gọi I là trung điểm CF. Chứng minh 3 điểm B, D, I thẳng hàng.
Khi kéo dài ED cắt BA tại F → EF chứa trung điểm D của AE
→ Tam giác AEFlà tam giác cân tại D
→ C và F đối xứng nhau qua D (vì D cũng nằm trên AC)
Suy ra: D là trung điểm của CF
→ Gọi I là trung điểm của CF ⇒ D cũng là trung điểm ⇒ D = I
⇒ 3 điểm B, D, I thẳng hàng ⇔ B, D, I cùng nằm trên đường thẳng BD
Đpcm
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


