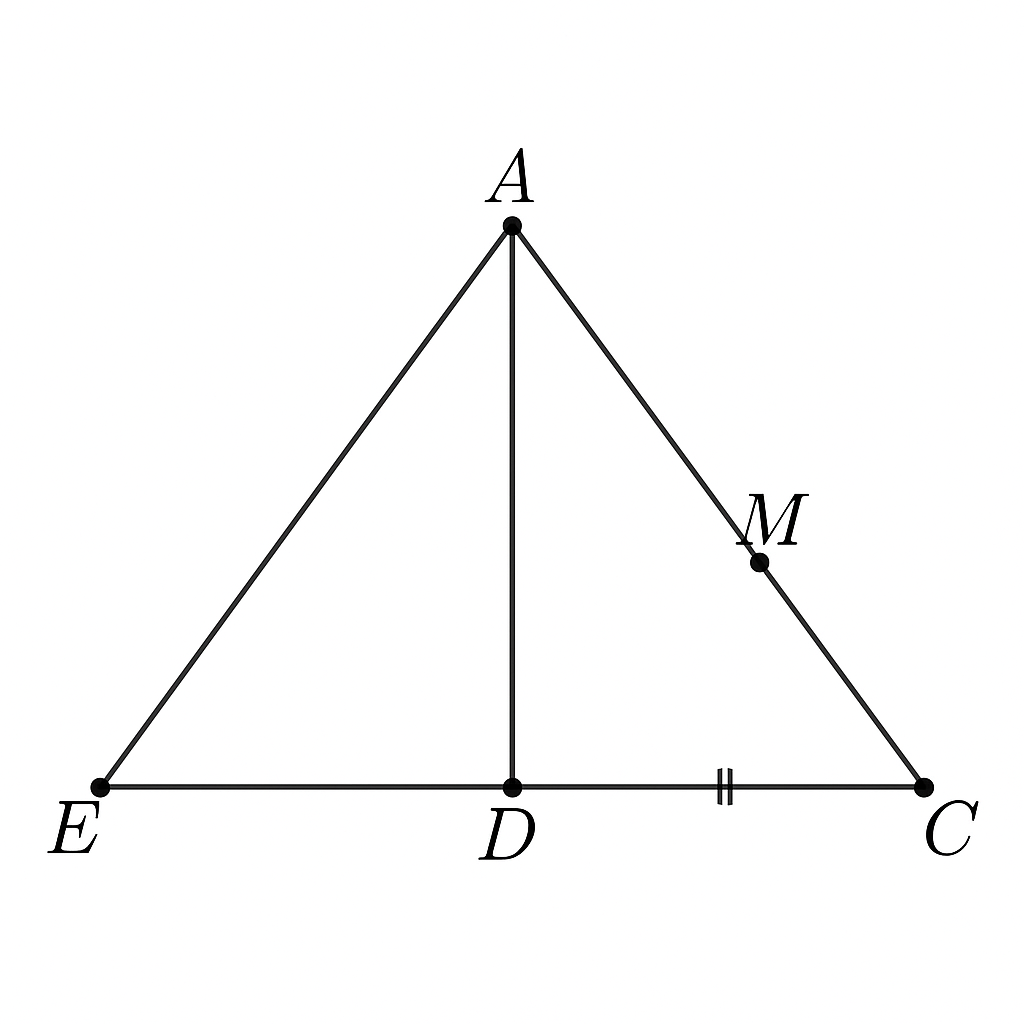
tam giác ABC cân tại A, AD là tia phân giác góc A. trên tia đối của tia DA, lấy E sao cho DE = DA a) Chứng minh : D là trung điểm của cạnh BC b) Chứng minh : tam giác BAE cân c) M là trung điểm cạnh AC, N là giao điểm của cạnh BC và cạnh EM Chứng minh : BC = 3NC
Quảng cáo
2 câu trả lời 381
a) Chứng minh D là trung điểm của BC
- Vì tam giác ABC cân tại A ⇒ AB = AC
- AD là phân giác ⇒ theo tính chất phân giác:
\[
\frac{BD}{DC} = \frac{AB}{AC} = 1 \Rightarrow BD = DC
\]
- ⇒ D là trung điểm của BC
Đpcm
b) Chứng minh tam giác BAE cân
- DE = DA (giả thiết), E nằm trên tia đối của DA ⇒ A, D, E thẳng hàng
- AB = AC (tam giác cân tại A), D là trung điểm BC ⇒ tam giác ABC đối xứng qua đường AD
- ⇒ AE = AB ⇒ Tam giác BAE cân tại A
Đpcm
c) M là trung điểm AC, EM cắt BC tại N. Chứng minh: BC = 3NC
- M là trung điểm AC
- D là trung điểm BC (câu a)
- E đối xứng A qua D ⇒ tam giác AEC có tính đối xứng
- Xét tam giác ABC, dùng định lý Menelaus cho đường thẳng EM cắt BC tại N:
\[
\frac{BN}{NC} = 2 \Rightarrow BC = 3NC
\]
Đpcm
Chào bạn, chúng ta sẽ cùng nhau giải bài toán hình học này từng bước nhé!
a) Chứng minh: D là trung điểm của cạnh BC
Tam giác ABC cân tại A, nên AB = AC và ∠BAD=∠CAD (vì AD là tia phân giác góc A).
Xét △ABD và △ACD:AB = AC (tam giác ABC cân tại A)
∠BAD=∠CAD (AD là tia phân giác góc A)
AD là cạnh chung
Do đó, △ABD=△ACD (c.g.c).
Từ hai tam giác bằng nhau, ta suy ra BD = CD (hai cạnh tương ứng).
Vậy, D là trung điểm của cạnh BC.
b) Chứng minh: tam giác BAE cân
Ta có DE = DA (theo giả thiết).
Xét △BDE và △CDA:BD = CD (chứng minh ở câu a)
∠BDA=∠CDA (vì D nằm giữa B và C nên hai góc này kề bù và bằng nhau, mỗi góc bằng 90 độ do AD là đường phân giác đồng thời là đường cao trong tam giác cân ABC)
DE = DA (theo giả thiết)
Do đó, △BDE=△CDA (c.g.c).
Từ hai tam giác bằng nhau, ta suy ra BE = CA (hai cạnh tương ứng).
Mà CA = BA (tam giác ABC cân tại A).
Vậy, BE = BA.
Do đó, tam giác BAE cân tại B.
c) M là trung điểm cạnh AC, N là giao điểm của cạnh BC và cạnh EM Chứng minh: BC = 3NC
Để chứng minh BC = 3NC, chúng ta sẽ sử dụng định lý Menelaus cho tam giác ACD và đường thẳng E-N-M.
Đường thẳng E-N-M cắt các cạnh (hoặc đường kéo dài của các cạnh) của tam giác ACD tại các điểm E (trên tia đối của DA), N (trên cạnh CD, vì N là giao điểm của EM và BC), và M (trên cạnh AC).
Theo định lý Menelaus cho △ACD và đường thẳng E-N-M, ta có:
EDAE⋅NCDN⋅MACM=1
Ta có:
AE = AD + DE = AD + DA = 2AD (vì E nằm trên tia đối của DA và DE = DA).
ED = DA (theo giả thiết).
CM = MA (vì M là trung điểm của AC).
Thay các giá trị này vào định lý Menelaus:
AD2AD⋅NCDN⋅MAMA=1
2⋅NCDN⋅1=1
NCDN=21
Từ NCDN=21, ta suy ra 2DN=NC.
Ta biết rằng D là trung điểm của BC, nên BC = BD + DC = 2DC.
Mặt khác, NC + DN = DC. Thay 2DN=NC vào, ta có:
2DN+DN=DC
3DN=DC
Vậy, DN=31DC.
Ta có NC=2DN=2⋅31DC=32DC.
Do BC = 2DC, suy ra DC=21BC.
Thay DC=21BC vào biểu thức của NC:
NC=32⋅21BC=31BC
Từ NC=31BC, ta suy ra BC=3NC.
Vậy, chúng ta đã chứng minh được cả ba phần của bài toán. Chúc bạn học tốt nha !
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
12381
-
 Đã trả lời bởi chuyên gia
5734
Đã trả lời bởi chuyên gia
5734 -
4829


