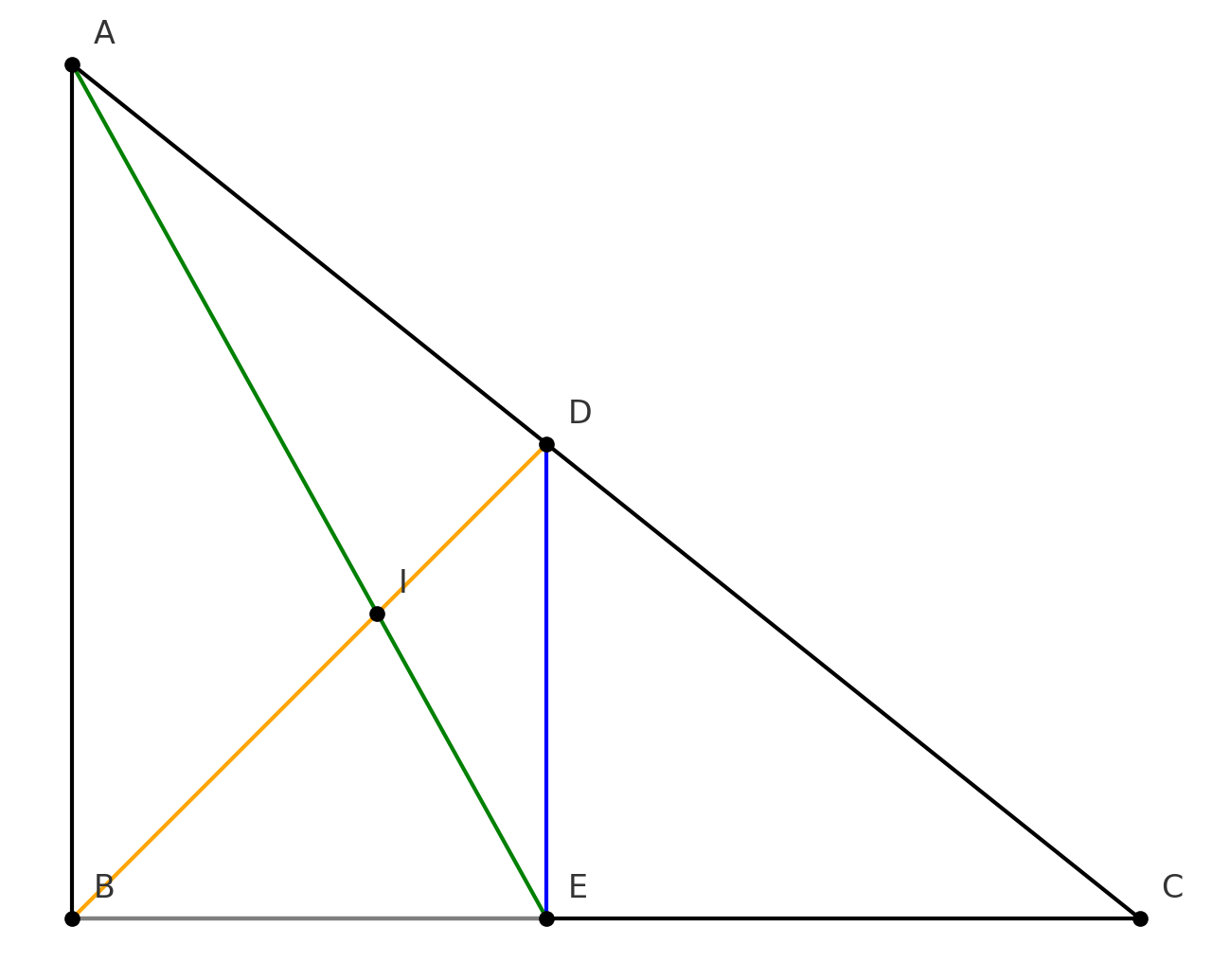
a) chứng minh Tam giác ABD=Tam giác EBD
b) Chứng minh BD là trung trực của AE
Quảng cáo
1 câu trả lời 216
a) Chứng minh tam giác \( \triangle ABD = \triangle EBD \)
Xét 2 tam giác: \( \triangle ABD \) và \( \triangle EBD \):
- Có cạnh chung: \( BD \)
- \( \angle ABD = \angle EBD \) (do BD là phân giác góc B nên chia góc \( \angle ABC \) thành 2 góc bằng nhau)
- \( AD = DE \): Ta chưa có dữ kiện này, nhưng có thể chứng minh 2 tam giác bằng nhau theo góc – cạnh – góc (g.c.g)
Xét:
- \( BD \) là cạnh chung
- \( \angle ABD = \angle EBD \) (do BD là phân giác)
- \( \angle ADB = \angle EDB \): do \( DE \perp BC \) và \( D \in AC \), \( E \in BC \), nên hai góc tại D này đối đỉnh nhau, bằng nhau.
⇒ \( \triangle ABD = \triangle EBD \) (theo góc – cạnh – góc)
Kết luận a:
\[
\boxed{\triangle ABD = \triangle EBD}
\]
b) Chứng minh BD là trung trực của AE
Từ câu a: \( \triangle ABD = \triangle EBD \) ⇒ các cạnh tương ứng bằng nhau:
→ \( AB = EB \), \( AD = DE \), và tam giác đối xứng qua BD
Ta xét tam giác \( \triangle ADE \):
- Có \( DE \perp BC \), tức là DE vuông góc với AE
- Và tam giác \( ABD = EBD \) ⇒ hai điểm A và E đối xứng nhau qua BD
⇒ BD vừa:
- đi qua trung điểm đoạn AE (do tam giác đối xứng)
- vuông góc với AE (vì DE ⊥ BC, kéo theo AE cắt BD tại I vuông góc)
Kết luận b:
\[
\boxed{\text{BD là đường trung trực của đoạn thẳng } AE}
\]
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515


