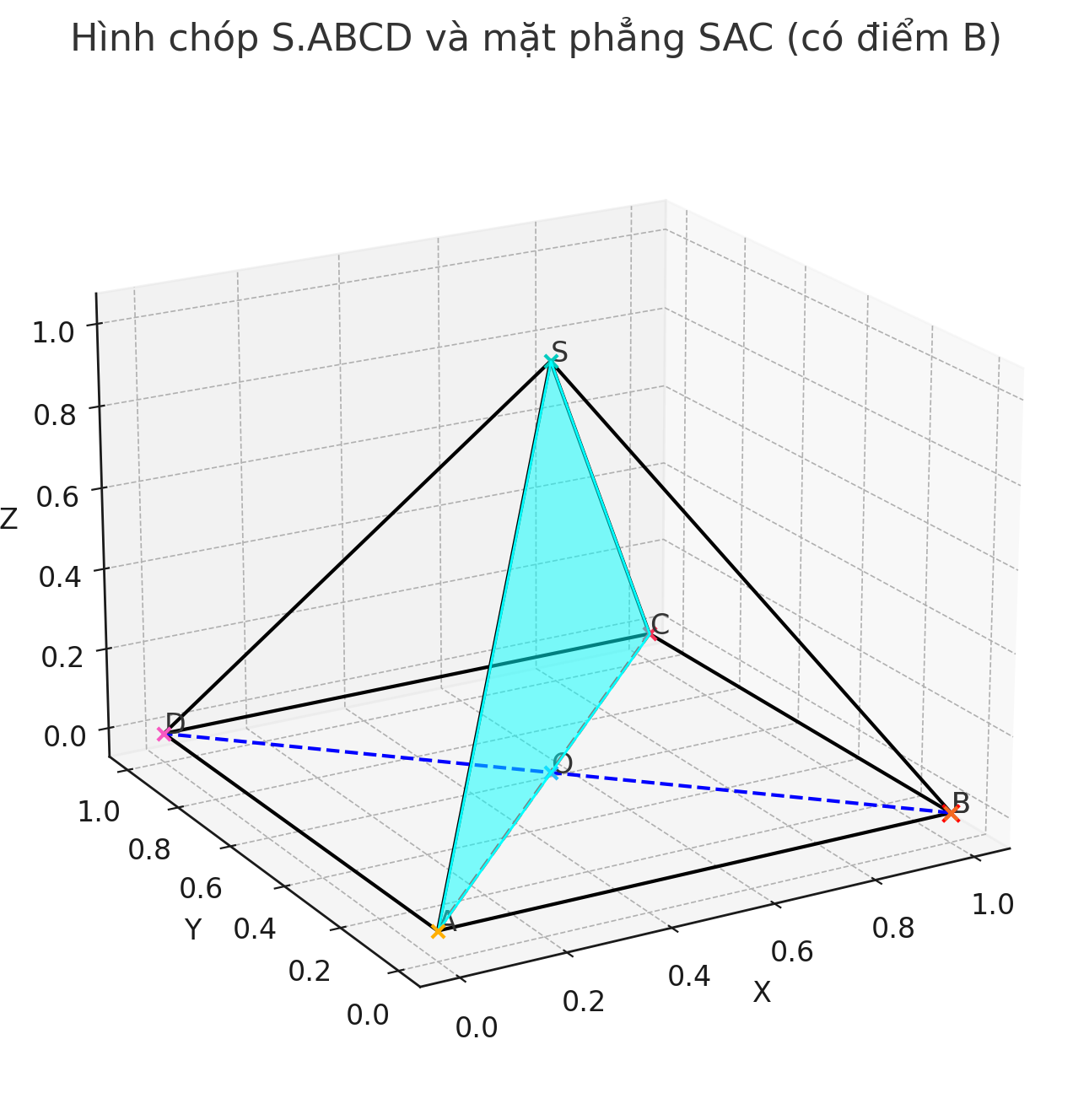
- Gọi \(A(0,0,0)\),
- \(B(a,0,0)\),
- \(C(a,a,0)\),
- \(D(0,a,0)\),
- Vậy \(O\) (giao điểm \(AC\) và \(BD\)) là trung điểm của \(AC\) và \(BD\), nên \(O\left(\frac{a}{2},\frac{a}{2},0\right)\),
- \(S\) nằm trên đường thẳng vuông góc với đáy tại \(O\), nên \(S\left(\frac{a}{2},\frac{a}{2},a\right)\) (vì \(SO = a\)).

Mặt phẳng (SAC) đi qua 3 điểm \(S, A, C\).

- \(\vec{SA} = (0-\frac{a}{2},0-\frac{a}{2},0-a) = \left(-\frac{a}{2},-\frac{a}{2},-a\right)\),
- \(\vec{SC} = (a-\frac{a}{2},a-\frac{a}{2},0-a) = \left(\frac{a}{2},\frac{a}{2},-a\right)\).

Tìm vectơ pháp tuyến bằng tích có hướng \(\vec{n} = \vec{SA} \times \vec{SC}\):

\[
\vec{n} = \begin{vmatrix}
\vec{i} & \vec{j} & \vec{k} \\
-\frac{a}{2} & -\frac{a}{2} & -a \\
\frac{a}{2} & \frac{a}{2} & -a \\
\end{vmatrix}
\]

\[
\vec{n} = \left((-a/2)(-a) - (-a/2)(-a)\right)\vec{i} - \left((-a/2)(-a) - (-a/2)(a/2)\right)\vec{j} + \left((-a/2)(a/2) - (-a/2)(-a/2)\right)\vec{k}
\]
Rút gọn:
- Thành phần \(i\): \((-a/2)(-a) - (-a/2)(-a) = 0\),
- Thành phần \(j\): \((-a/2)(-a) - (-a/2)(a/2) = (a^2/2) - (-a^2/4) = (3a^2/4)\),
- Thành phần \(k\): \((-a/2)(a/2) - (-a/2)(-a/2) = (-a^2/4) - (a^2/4) = -a^2/2\).

Vậy:
\[
\vec{n} = \left(0, -\frac{3a^2}{4}, -\frac{a^2}{2}\right)
\]

Chia tiêu chuẩn để đơn giản hóa: lấy hệ số chung \(a^2/4\) ra ngoài:
\[
\vec{n} = \frac{a^2}{4}(0, -3, -2)
\]
Ta bỏ \(a^2/4\) vì mặt phẳng chỉ cần tỉ lệ đúng, vậy vectơ pháp tuyến có thể lấy:
\[
\vec{n} = (0, -3, -2)
\]

Phương trình mặt phẳng (SAC):
Dùng điểm \(S\left(\frac{a}{2},\frac{a}{2},a\right)\):

\[
0(x-\frac{a}{2}) -3(y-\frac{a}{2}) -2(z-a) = 0
\]
Rút gọn:
\[
-3\left(y-\frac{a}{2}\right) -2\left(z-a\right) = 0
\]
\[
-3y + \frac{3a}{2} -2z +2a = 0
\]
\[
-3y -2z +\frac{7a}{2} = 0
\]
hoặc:
\[
3y + 2z = \frac{7a}{2}
\]

Công thức khoảng cách từ điểm \(M(x_0,y_0,z_0)\) đến mặt phẳng \(Ax + By + Cz + D = 0\) là:

\[
d = \frac{|Ax_0 + By_0 + Cz_0 + D|}{\sqrt{A^2+B^2+C^2}}
\]

Với mặt phẳng \(3y + 2z - \frac{7a}{2} = 0\), ta có:
- \(A=0\),
- \(B=3\),
- \(C=2\),
- \(D=-\frac{7a}{2}\).

Thế \(B(a,0,0)\) vào:

\[
d = \frac{|0\cdot a + 3\cdot 0 + 2\cdot 0 - \frac{7a}{2}|}{\sqrt{0^2+3^2+2^2}} = \frac{|\frac{-7a}{2}|}{\sqrt{9+4}} = \frac{7a/2}{\sqrt{13}}
\]

Vậy khoảng cách cần tìm là:

\[
{\frac{7a}{2\sqrt{13}}}
\]