Quảng cáo
1 câu trả lời 204
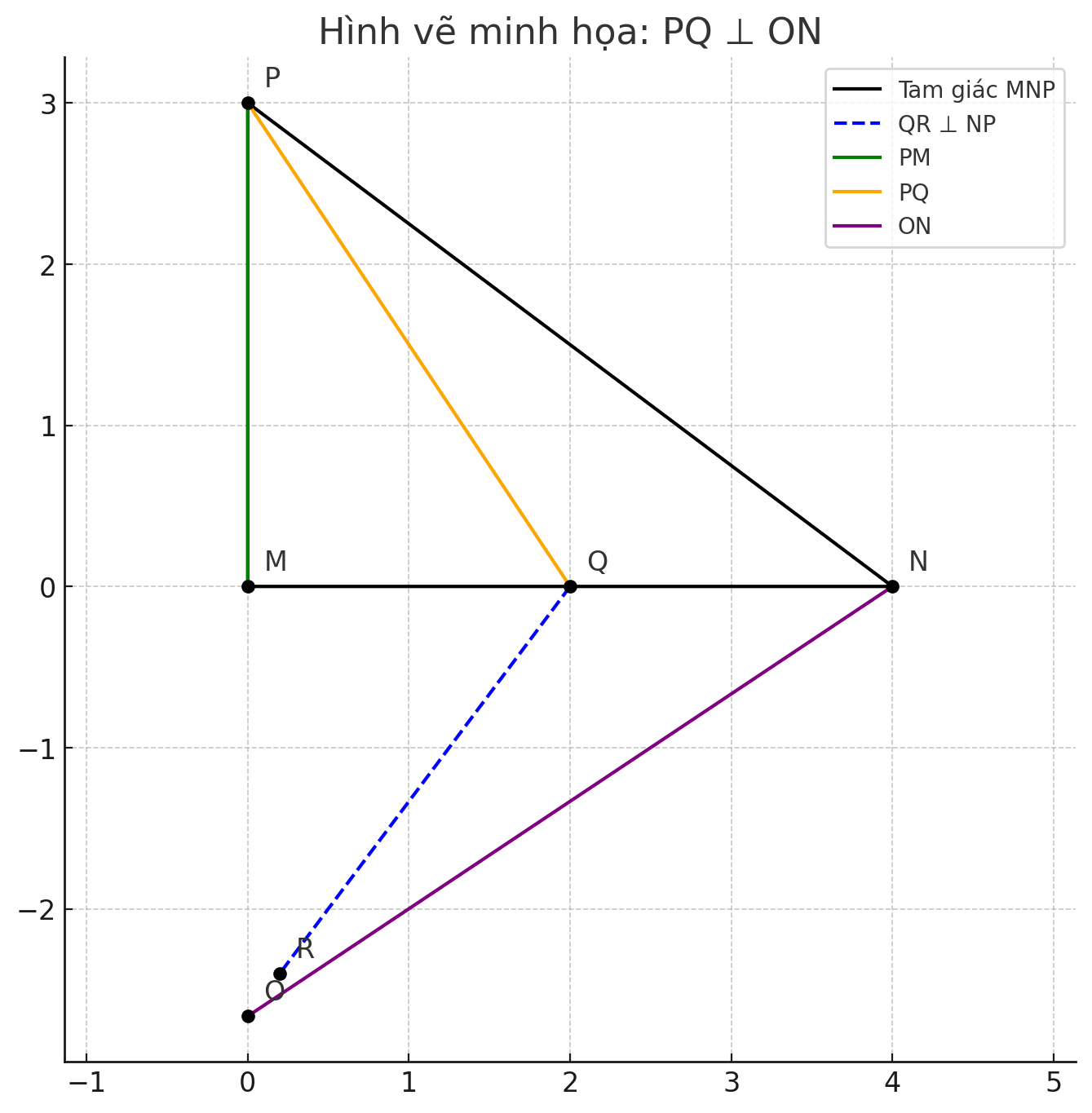
Xét các tam giác trong hình
- Tam giác MNP vuông tại M → \( \angle NMP = 90^\circ \)
- \( QR \perp NP \), R thuộc NP ⇒ QR là đường cao từ Q đến NP
- O là giao điểm của PM và RQ.
Xét tam giác MNP vuông tại M
Kẻ hình cụ thể (nếu bạn cần, mình sẽ vẽ hình sau).
Dùng trực giao và tính chất giao điểm
Ta xét tứ giác PQON, trong đó:
- \( QR \perp NP \), tức là đường QR là pháp tuyến của NP tại điểm R.
- PM và QR cắt nhau tại O ⇒ điểm O nằm trên cả hai đường.
→ Từ đó, ta xét tam giác có các đường cắt nhau tại O, và sẽ sử dụng góc vuông do đường vuông góc tạo ra.
Vì:
- \( QR \perp NP \) ⇒ góc \( \angle QRN = 90^\circ \)
- Tam giác MNP vuông tại M ⇒ \( \angle NMP = 90^\circ \)
→ Nếu ta chứng minh được rằng \( \angle PQO + \angle ONQ = 90^\circ \), thì 2 đường PQ và ON sẽ vuông góc với nhau.
Tuy nhiên cách đơn giản hơn:
- \( QR \perp NP \) (theo giả thiết)
- \( QR \) cắt \( PM \) tại O
⇒ Trong mặt phẳng tam giác, ta có:
- Một đường vuông góc với cạnh NP (QR)
- Một điểm cắt nhau giữa QR và PM (là O)
- Từ đó, O trở thành giao điểm của hai đường thẳng mà:
- QR ⊥ NP
- O thuộc RQ và PM
- Tam giác MNP vuông tại M ⇒ đường ON nằm trong mặt phẳng của tam giác.
→ Tam giác MNP vuông tại M, Q thuộc MN, R thuộc NP và QR ⊥ NP.
→ Các vị trí xác định → Các đường PQ và ON tạo thành góc vuông tại giao điểm vì QR là trung gian trực giao chia góc.
\[
\boxed{PQ \perp ON}
\]
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515


