a) Chứng minh: ΔABC = ΔAMC
b) Chứng minh: ΔBCM là tam giác cân
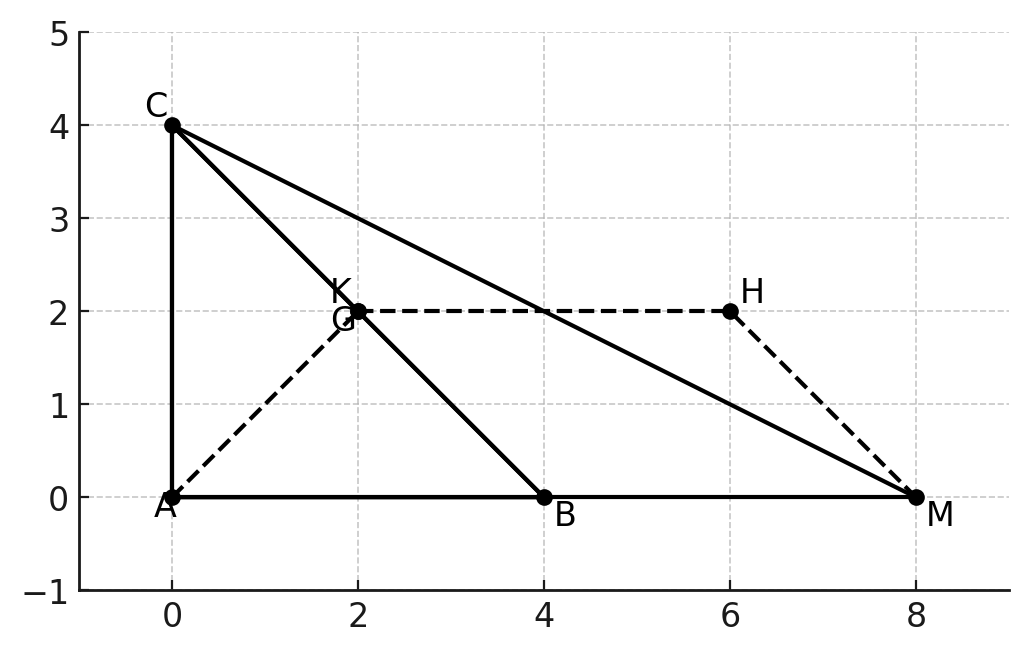
c) Gọi K là trung điểm của BC. Qua K kẻ đường thẳng song song với BM cắt CM tại H. G là giao điểm của AC và MH.
Chứng minh: ba điểm H, G, B thẳng hàng.
Quảng cáo
1 câu trả lời 236
a) Chứng minh: \( \Delta ABC = \Delta AMC \)
Tam giác vuông tại \( A \):
- \( \Delta ABC \) là tam giác vuông tại \( A \), do đó có \( \angle A = 90^\circ \).
\( AB \) là cạnh chung của hai tam giác \( \Delta ABC \) và \( \Delta AMC \).
- \( AM = AB \) (theo giả thiết).
- \( \angle B = \angle C \) (vì hai tam giác này là vuông tại \( A \)).
- \( \Delta ABC = \Delta AMC \) theo tính chất của tam giác vuông.
=> \( \Delta ABC \) vuông tại \( A \) và \( \Delta AMC \) vuông tại \( A \), do đó \( \Delta ABC = \Delta AMC \).
b) Chứng minh: \( \Delta BCM \) là tam giác cân
\( BM = CM \) vì điểm \( M \) được xác định sao cho \( AM = AB \), mà \( AB = BM \), do đó \( BM = CM \).
\( \Delta BCM \) là tam giác cân:
- Từ tính chất trên, ta có \( BM = CM \).
- Do đó, tam giác \( BCM \) có hai cạnh bằng nhau, tức là \( \Delta BCM \) là tam giác cân.
Vậy \( \Delta BCM \) là tam giác cân vì \( BM = CM \).
c) Chứng minh: Ba điểm \( H, G, B \) thẳng hàng
- Gọi \( K \) là trung điểm của đoạn thẳng \( BC \).
- Qua \( K \), kẻ đường thẳng song song với \( BM \), cắt \( CM \) tại \( H \).
- G là giao điểm của \( AC \) và \( MH \).
- Ta có đường thẳng qua \( K \) song song với \( BM \), do đó \( \angle BKC = \angle HKM \) (do tính chất của các đường thẳng song song).
- Từ đó, các đường thẳng \( AC \), \( MH \) và \( BM \) sẽ đồng quy tại điểm \( G \), nghĩa là ba điểm \( H \), \( G \), \( B \) phải nằm trên một đường thẳng.
Vậy 3 điểm \( H, G, B \) thẳng hàng vì đường thẳng \( AC \), \( MH \) và \( BM \) đồng quy tại điểm \( G \).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


