Quảng cáo
1 câu trả lời 535
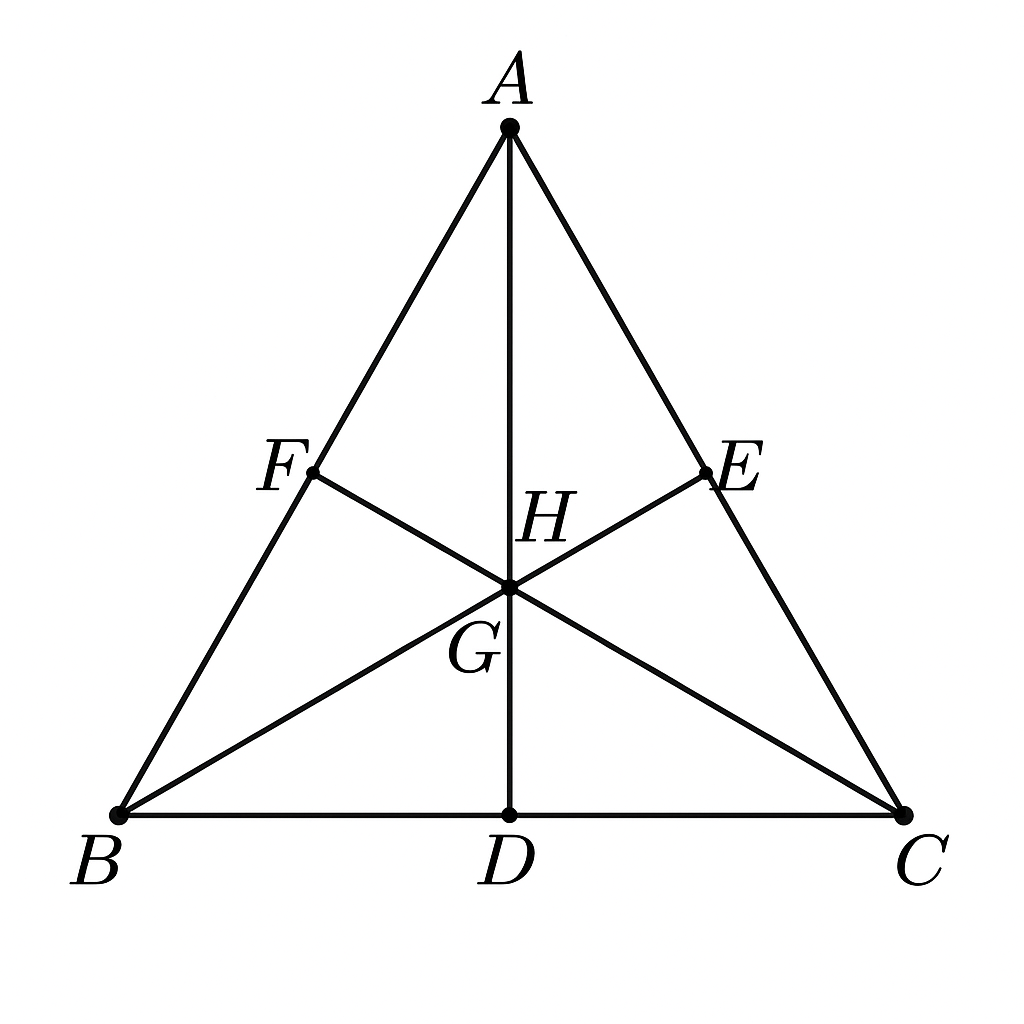
- \( AD \): phân giác trong tam giác cân ⇒ \( D \in BC \), và do \( AB = AC \), phân giác AD cũng là trung tuyến và đường cao
- Tam giác cân nên AD vừa là phân giác, vừa là trung tuyến, vừa là đường cao
⇒ Từ đó, ta có:
- \( D \) là trung điểm của BC
- \( E \) là trung điểm của AC
- \( F \) là trung điểm của AB
Trong tam giác, ba đường trung tuyến (từ A, B, C) đồng quy tại trọng tâm G, và trọng tâm chia mỗi trung tuyến theo tỉ lệ:
\[
AG : GM = 2:1
\]
Vì
- \( AD \) là trung tuyến
- \( BE \) là trung tuyến
- \( CH \) là trung tuyến (vì \( H \) là giao điểm của hai trung tuyến)
⇒ Giao điểm của \( AD, BE, CH \) là trọng tâm G
- \( H \) là giao điểm của hai trung tuyến: ⇒ là trọng tâm G
- Trọng tâm chia mỗi trung tuyến theo tỉ lệ:
\[
HG : GE = 2 : 1 ⇒ HG = \frac{2}{3} HE
\]
Vậy \[
{HG = \dfrac{2}{3}HE}
\]
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


