Thoảng Mai
Hỏi từ APP VIETJACK
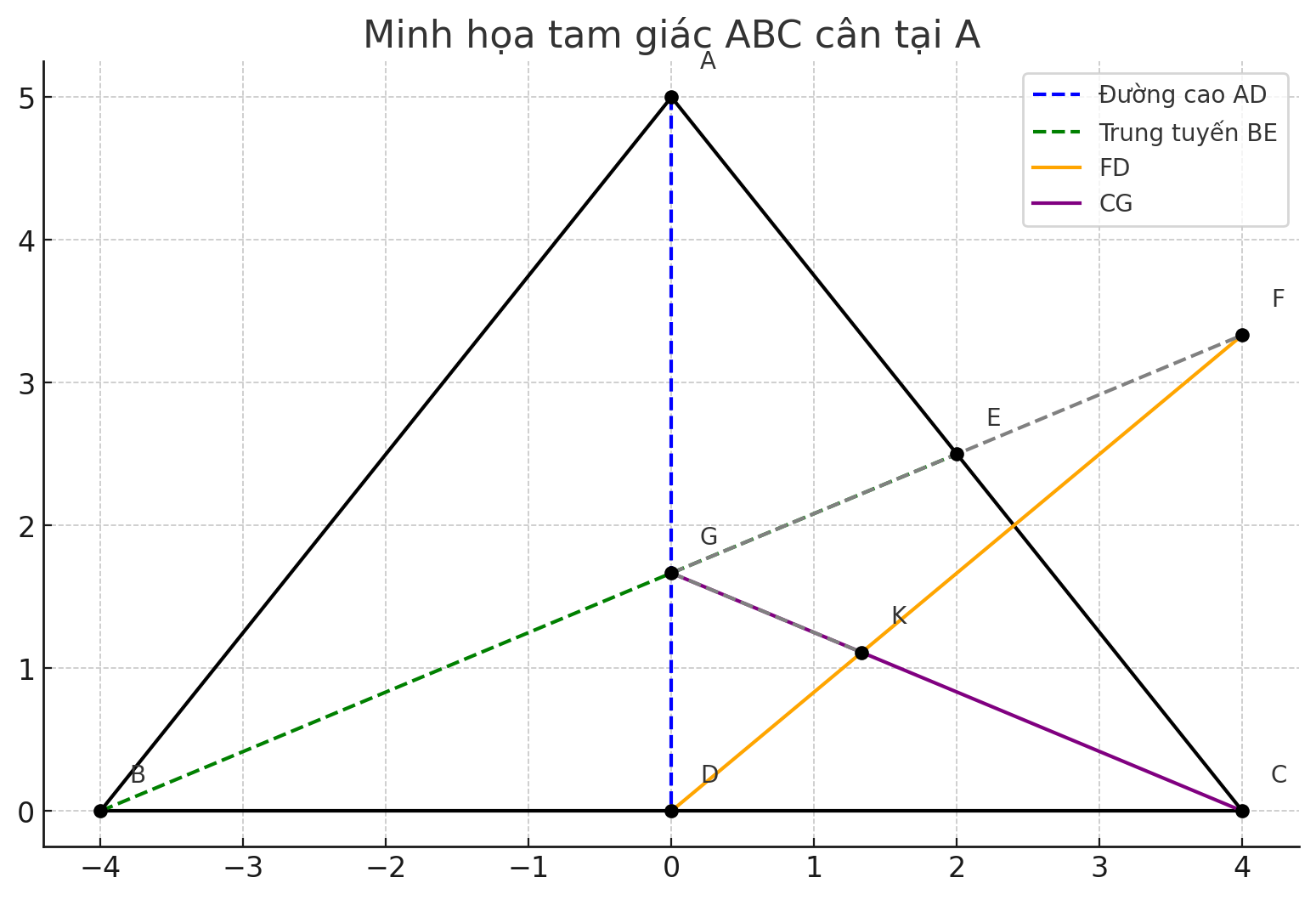
Cho tam giác ABC cân tại coa đường cao AD và đường trung tuyến BE cắt nhau tai G.
a) CM: TAM GIÁC ABG = TAM GIÁC ACG ?
Trên tia đối của tia EB lấy điểm F sao cho GE=EF. GỌI K là giao điểm của FD với CG .CM : GF=3GK?
a) CM: TAM GIÁC ABG = TAM GIÁC ACG ?
Trên tia đối của tia EB lấy điểm F sao cho GE=EF. GỌI K là giao điểm của FD với CG .CM : GF=3GK?
Quảng cáo
2 câu trả lời 730
2 tháng trước
a) Chứng minh △ABG=△ACG
Xét hai tam giác ABG và ACG:
- Cạnh chung: AG
- AB=AC (do tam giác cân tại A)
- Góc ∠ABG=∠ACG vì G nằm trên trung tuyến và đường cao (đối xứng nhau qua trục AD)
→ Hai tam giác có:
- Hai cạnh tương ứng bằng nhau
- Góc xen giữa bằng nhau
⇒ Đồng dạng, thậm chí bằng nhau (cạnh – góc – cạnh)
△ABG=△ACG
b) Gọi F là điểm đối xứng của G qua E (vì GE=EF).
Gọi K=FD∩CG. Chứng minh: GF=3GK
Vì GF=2GE, mà GK=13GF
→ GF=3GK
GF=3GK
Quảng cáo
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK112000
-
78256
-
56023
Gửi báo cáo thành công!



