Quảng cáo
1 câu trả lời 466
a) Chứng minh:
\[
MA + MB + MC > \frac{AB + BC + CA}{2}
\]
Áp dụng bất đẳng thức tam giác:
- Trong mỗi tam giác, tổng hai cạnh luôn lớn hơn cạnh còn lại
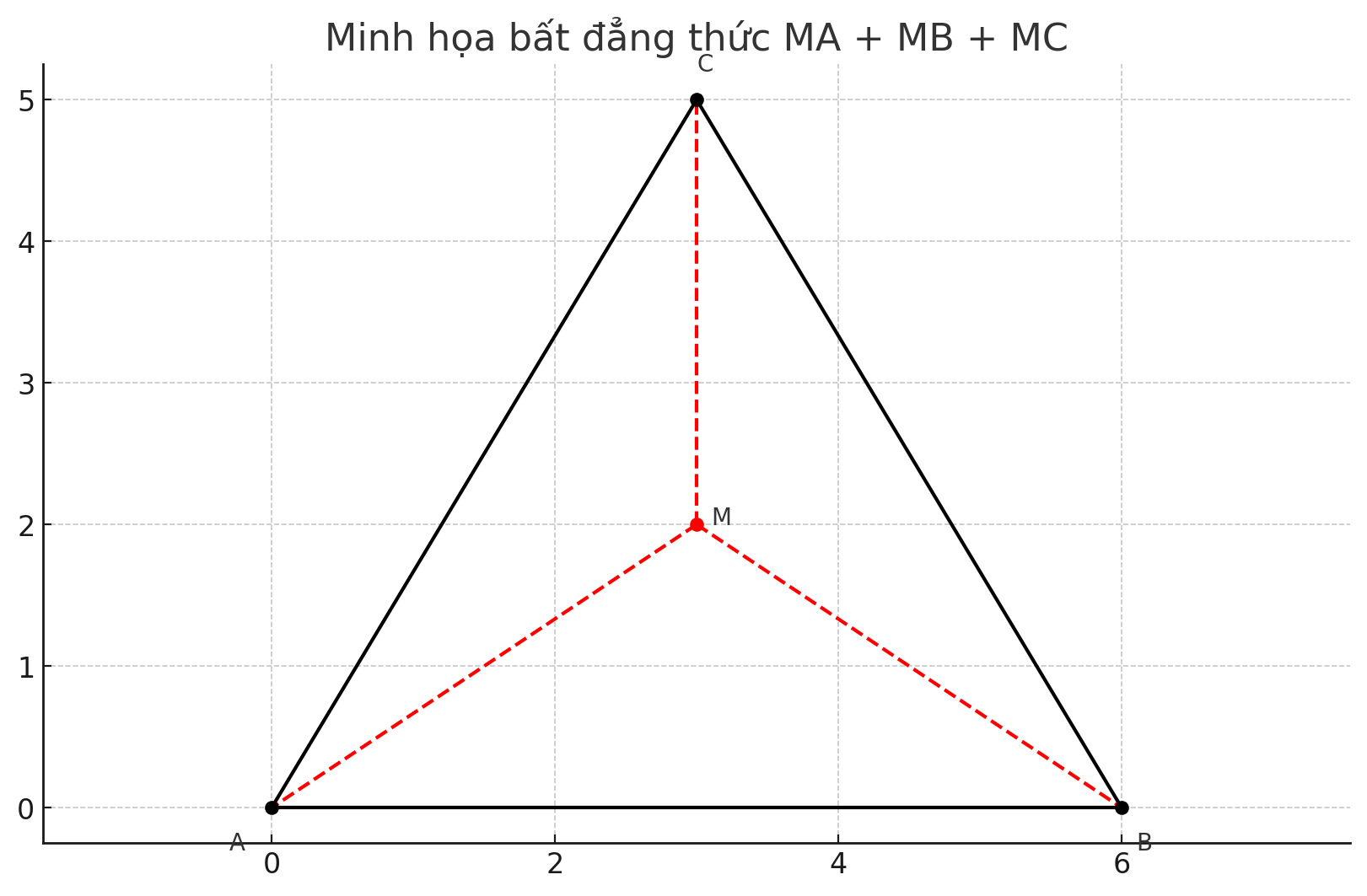
Bây giờ, xét các tam giác tạo bởi điểm \( M \):
- Trong tam giác \( ABM \):
\( MA + MB > AB \)
- Trong tam giác \( BCM \):
\( MB + MC > BC \)
- Trong tam giác \( CAM \):
\( MC + MA > CA \)
Cộng vế theo vế:
\[
(MA + MB) + (MB + MC) + (MC + MA) > AB + BC + CA
\]
\[
2(MA + MB + MC) > AB + BC + CA
\]
Chia hai vế cho 2:
\[
MA + MB + MC > \frac{AB + BC + CA}{2}
\]
Đpcm
b) Chứng minh:
\[
MA + MB + MC < AB + BC + CA
\]
- Do điểm \( M \) nằm trong tam giác ABC, nên nó không trùng với các đỉnh ⇒ các đoạn \( MA, MB, MC \) nhỏ hơn độ dài đi theo các cạnh của tam giác từ A → B → C → A
- Đường đi từ A → M → B ngắn hơn đường đi theo cạnh AB,
tương tự các đoạn còn lại.
Cụ thể, theo nguyên lý đường gấp khúc lớn hơn đường thẳng:
\[
MA + MB < AB + (một phần nhỏ)
\]
\[
MB + MC < BC + (một phần nhỏ)
\]
\[
MC + MA < CA + (một phần nhỏ)
\]
Khi cộng 3 đoạn MA, MB, MC lại, ta được tổng nhỏ hơn đường bao tam giác ABC.
Vì vậy:
\[
MA + MB + MC < AB + BC + CA
\]
Đpcm
- \( MA + MB + MC > \dfrac{AB + BC + CA}{2} \)
- \( MA + MB + MC < AB + BC + CA \)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120962
-
 Đã trả lời bởi chuyên gia
81713
Đã trả lời bởi chuyên gia
81713 -
 Đã trả lời bởi chuyên gia
59651
Đã trả lời bởi chuyên gia
59651 -
 Đã trả lời bởi chuyên gia
39669
Đã trả lời bởi chuyên gia
39669


