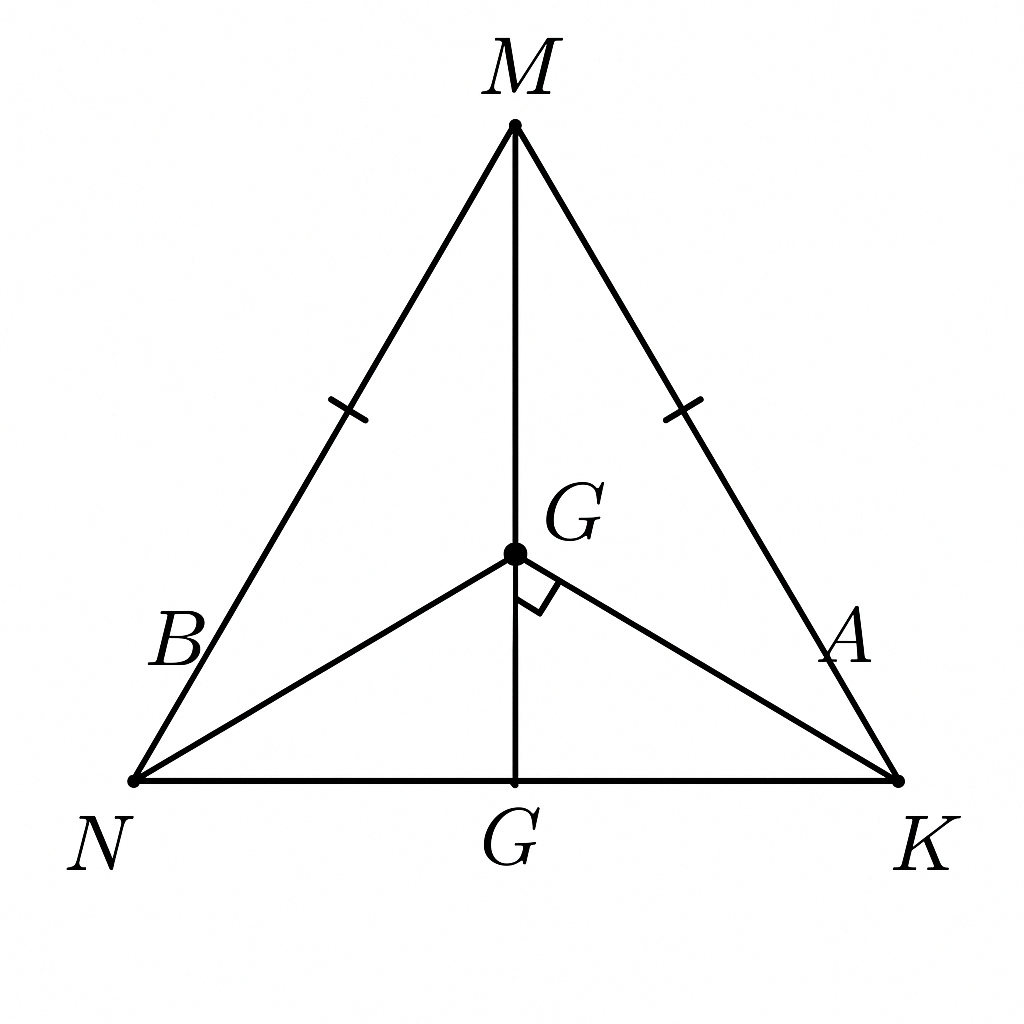
Cho ∆MNK cân tại M. Các đường trung tuyến NA, KB cắt nhau tại G a) Chứng minh ∆B...

meiho kaishin

đã hỏi trong Lớp 7 Toán học

· 21:46 15/04/2025

Đề kiểm tra Học kì 2 Toán 7

Cho $∆$ MNK cân tại M. Các đường trung tuyến NA, KB cắt nhau tại G

a) Chứng minh $∆$ BNK= $∆$ AKN

b) Chứng minh $∆$ GNK cân

c) Chứng minh MG vuông NK

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

1 câu trả lời 173

Sang Phạm

8 tháng trước

a) Chứng minh $ \Delta BNK = \Delta AKN $

Ta xét hai tam giác $ \Delta BNK $ và $ \Delta AKN $:

- Cạnh chung: $ NK $
- $ B $ là trung điểm $ MN $, $ A $ là trung điểm $ MK $ (vì NA, KB là trung tuyến)
- Tam giác $ MNK $ cân tại M, nên:
\[
MN = MK \Rightarrow MB = MA \quad \text{(do B, A là trung điểm)}
\]

→ Tam giác $ \Delta BNK $ và $ \Delta AKN $ có:
- $ MB = MA $
- $ BN = AK $ (vì là trung tuyến ứng với hai cạnh bằng nhau)
- Chung cạnh $ NK $

⇒ $ \Delta BNK = \Delta AKN $ (theo trường hợp cạnh – cạnh – cạnh)

Đpcm

b) Chứng minh tam giác $ \Delta GNK $ cân

Ta cần chứng minh $ GN = GK $

Do:
- $ G $ là giao điểm hai đường trung tuyến → là trọng tâm tam giác
- Trọng tâm G chia mỗi trung tuyến theo tỉ lệ $ 2:1 $

→ Vì tam giác MNK cân tại M ⇒ $ MB = MA $, nên:
- Trung tuyến từ $ K $: $ KB $
- Trung tuyến từ $ N $: $ NA $

→ $ G $ chia $ KB $ và $ NA $ theo cùng tỉ lệ
→ Từ tính chất đối xứng, tam giác $ GNK $ sẽ cân tại G

Có thể chứng minh cụ thể bằng vector hoặc toạ độ, nhưng về hình học:
- Do $ \Delta BNK = \Delta AKN $ (ở câu a)
→ hai tam giác này ghép lại đối xứng qua đường trung tuyến từ M
→ Trọng tâm G nằm trên trục đối xứng
→ Suy ra $ GN = GK $

Tam giác GNK cân tại G — đpcm

c) Chứng minh $ MG \perp NK $

Ta cần chứng minh đường từ đỉnh M đến trọng tâm G vuông góc với đáy NK.

Gợi ý:
- Do $ \Delta MNK $ cân tại M ⇒ trục đối xứng là đường từ M đi qua trung điểm đáy NK
- Mà trọng tâm G nằm trên trục đối xứng đó
→ $ MG $ chính là đường trung tuyến ứng với đáy NK trong tam giác cân

⇒ Trong tam giác cân, đường trung tuyến từ đỉnh đồng thời là đường cao

→ MG vừa là trung tuyến, vừa vuông góc với đáy NK

$ MG \perp NK $ — Đpcm

a) $ \Delta BNK = \Delta AKN $ (c.g.c)
b) $ \Delta GNK $ cân tại G
c) $ MG \perp NK $