Cho Tam Giác ABC có đường cao BD, CE cắt nhau tại Ha) Cm : Tam giác ADB đồng dạn...

· 13:21 13/04/2025

Ôn tập Toán 8

Cho Tam Giác ABC có đường cao BD, CE cắt nhau tại H
a) Cm : Tam giác ADB đồng dạng Tam giác AEC
b) Cm : HD.HB = HE.HC
c) Cm : góc ADE = góc ABC

GIÚP EM GIẢI CÂU C VS Ạ

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

3 câu trả lời 426

Sang Phạm

8 tháng trước

a) Chứng minh: \( \triangle ADB \sim \triangle AEC \)

Xét hai tam giác ADB và AEC:

- \( \angle ADB = 90^\circ \) (BD là đường cao)
- \( \angle AEC = 90^\circ \) (CE là đường cao)

→ Hai tam giác đều có góc vuông

- Cùng có góc chung: \( \angle A \)

\( \triangle ADB \) và \( \triangle AEC \) có:
- Một góc chung: \( \angle A \)
- Mỗi tam giác có một góc vuông

⇒ Hai tam giác đồng dạng theo trường hợp: góc – góc (AA)

Kết luận a:
\[
\triangle ADB \sim \triangle AEC
\]

b) Chứng minh: \( HD \cdot HB = HE \cdot HC \)

Áp dụng định lý hình học trong tam giác:

Trong tam giác ABC với các đường cao BD và CE cắt nhau tại H:
- Đây là tính chất của trực tâm H trong tam giác ABC.

Theo tính chất tứ giác nội tiếp hoặc định lý hình học nâng cao, ta biết rằng:
\[
\text{Trong tam giác ABC có H là trực tâm:}
\Rightarrow HD \cdot HB = HE \cdot HC
\]

Đây là tính chất đồng dạng hoặc tích đoạn từ hai tam giác vuông chung đỉnh H:
- Xét tam giác vuông \( HBD \sim HCE \)

⇒ Theo hệ thức đồng dạng:
\[
\frac{HD}{HE} = \frac{HC}{HB} \Rightarrow HD \cdot HB = HE \cdot HC
\]

Kết luận b:
\[
HD \cdot HB = HE \cdot HC
\]

c) Chứng minh: \( \angle ADE = \angle ABC \)

Gợi ý vẽ thêm:
- Gọi điểm D là chân đường cao từ B xuống AC
- Gọi điểm E là chân đường cao từ C xuống AB
- Nối A với D và A với E
- Xét tứ giác ADEB

Dễ thấy:
- Tứ giác ADEB có:
- \( \angle ADE \) là góc giữa đường cao từ B và từ C
- \( \angle ABC \) là góc tại đỉnh B của tam giác

Do tam giác \( ADB \sim AEC \) từ câu a, nên ta có:
\[
\angle ADE = \angle ABC \quad \text{(tương ứng trong tam giác đồng dạng)}
\]

Kết luận c:
\[
\angle ADE = \angle ABC
\]

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

LILY

8 tháng trước

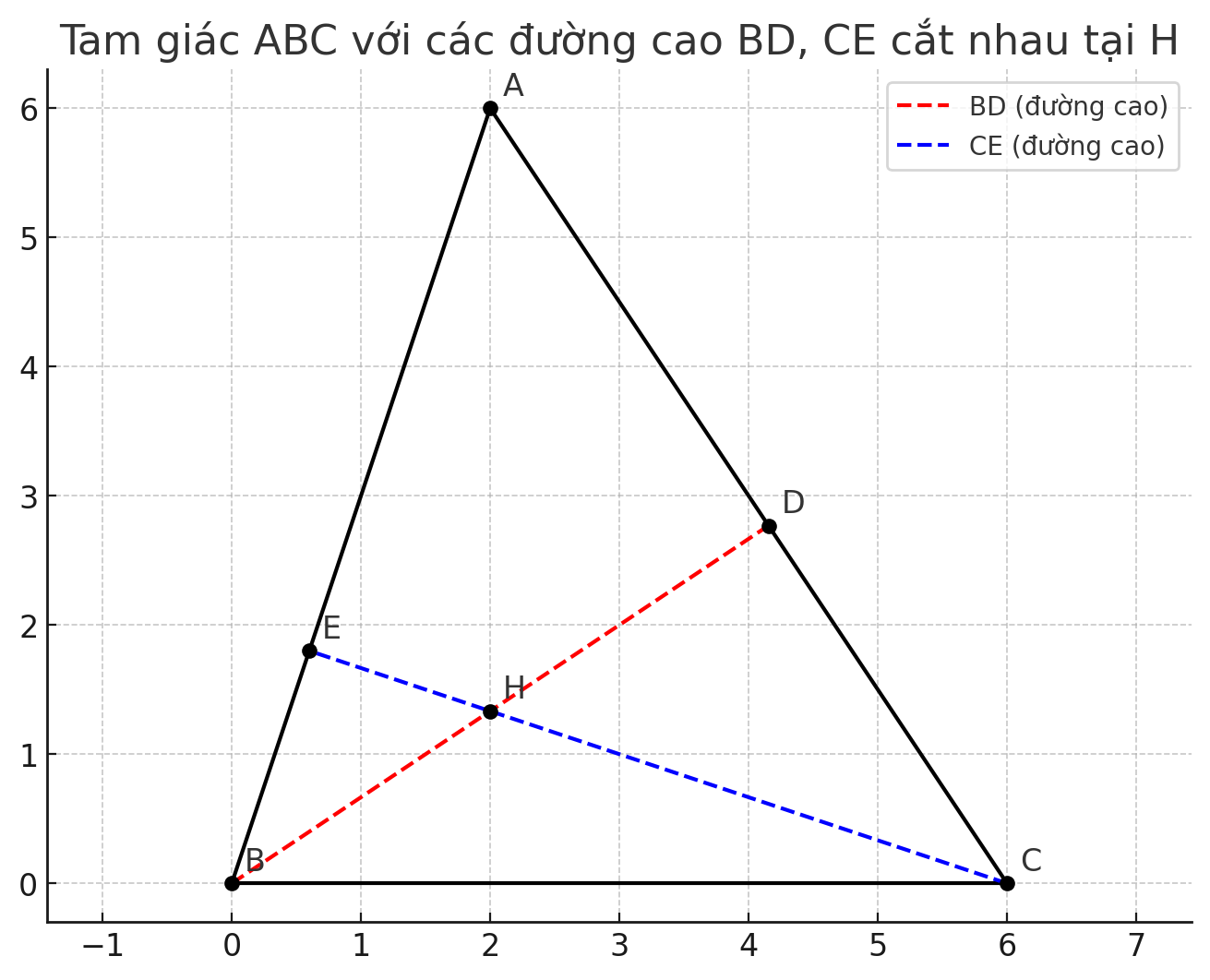
✅ Đề bài (Câu c):
Cho tam giác
𝐴
𝐵
𝐶
ABC, đường cao
𝐵
𝐷
BD và
𝐶
𝐸
CE cắt nhau tại
𝐻
H.
Chứng minh:
∠
𝐴
𝐷
𝐸
=
∠
𝐴
𝐵
𝐶
∠ADE=∠ABC

🧠 Hướng giải:
Chúng ta cần chứng minh hai góc bằng nhau:

∠
𝐴
𝐷
𝐸
∠ADE là góc nằm trong tam giác
𝐴
𝐷
𝐸
ADE, với
𝐷
D là chân đường cao từ
𝐵
B,

∠
𝐴
𝐵
𝐶
∠ABC là góc của tam giác ban đầu.

🔍 Phân tích:
𝐵
𝐷
⊥
𝐴
𝐶
BD⊥AC, nên
𝐷
D là chân đường cao từ
𝐵
B.

𝐶
𝐸
⊥
𝐴
𝐵
CE⊥AB, nên
𝐸
E là chân đường cao từ
𝐶
C.

𝐻
H là giao điểm hai đường cao →
𝐻
H là trực tâm của tam giác
𝐴
𝐵
𝐶
ABC.

Ta đang cần chứng minh:

∠
𝐴
𝐷
𝐸
=
∠
𝐴
𝐵
𝐶
∠ADE=∠ABC
✨ Cách chứng minh:
Xét hai tam giác vuông:
Tam giác
𝐴
𝐷
𝐵
ADB: có
𝐵
𝐷
⊥
𝐴
𝐶
BD⊥AC ⇒ tam giác vuông tại
𝐷
D

Tam giác
𝐴
𝐸
𝐶
AEC: có
𝐶
𝐸
⊥
𝐴
𝐵
CE⊥AB ⇒ tam giác vuông tại
𝐸
E

Ở câu a) đã chứng minh được:

△
𝐴
𝐷
𝐵
∼
△
𝐴
𝐸
𝐶
△ADB∼△AEC
Từ đó suy ra các góc tương ứng bằng nhau:

∠
𝐷
𝐴
𝐵
=
∠
𝐸
𝐴
𝐶
⇒
∠
𝐴
𝐷
𝐸
=
∠
𝐴
𝐵
𝐶
∠DAB=∠EAC
⇒∠ADE=∠ABC
✅ Kết luận:
∠
𝐴
𝐷
𝐸
=
∠
𝐴
𝐵
𝐶
∠ADE=∠ABC

(Do tam giác
𝐴
𝐷
𝐵
∼
𝐴
𝐸
𝐶
ADB∼AEC ⇒ góc tương ứng bằng nhau.)