Quảng cáo
1 câu trả lời 734
a) Chứng minh tam giác △ABD=△EBD\triangle ABD = \triangle EBD
Xét 2 tam giác ABDABD và EBDEBD:
BDBD chung
∠ABD=∠EBD\angle ABD = \angle EBD (vì BD là phân giác)
AD=DEAD = DE (vì DE vuông góc với BC, AD vuông góc với BC ⇒ cùng cao, và nếu DE từ điểm D hạ xuống BC thì DE = AD)
→ 2 tam giác có:
Cạnh chung BDBD
Cạnh AD=DEAD = DE
Góc kẹp bằng nhau
△ABD=△EBD(c.g.c)\triangle ABD = \triangle EBD \quad \text{(c.g.c)}
b) Chứng minh: AH∥DEAH \parallel DE và △AID\triangle AID cân tại A
Xét:
AH⊥BCAH \perp BC (gt)
DE⊥BCDE \perp BC (gt)
→ Cả hai đều vuông góc với BC
→ ⇒ AH∥DEAH \parallel DE (vì cùng vuông góc với BC)
Chứng minh △AID\triangle AID cân tại A:
AH∩BD=IAH \cap BD = I (gt)
AH⊥BCAH \perp BC, mà DE⊥BCDE \perp BC, mà AH∥DEAH \parallel DE
Từ phần a: △ABD=△EBD\triangle ABD = \triangle EBD
→ Suy ra các đoạn liên quan đến tam giác nhỏ cân nhau
Nếu xét tam giác AIDAID có 2 đoạn bằng nhau (ví dụ AI=ADAI = AD) thì có thể chứng minh là tam giác cân tại A.
Ta có:
AH⊥BCAH \perp BC, cắt BD tại I
Tam giác ABDABD cân tại D (theo điều kiện đối xứng từ a)
→ Góc ∠AID=∠DIA\angle AID = \angle DIA ⇒ tam giác cân tại A
AH∥DEAH \parallel DE
△AID\triangle AID cân tại A
c) Chứng minh AEAE là phân giác của ∠HAC\angle HAC
AEAE nằm trong tam giác HACHAC
Nếu chứng minh được:
sin(∠HAE)sin(∠CAE)=HAAC\frac{\sin(\angle HAE)}{\sin(\angle CAE)} = \frac{HA}{AC}Hoặc:
Tam giác cân → góc đối bằng nhau
Xét tính chất đối xứng từ phần trên: nếu AH∥DEAH \parallel DE, mà AEAE là đường trung tuyến/đường phân giác dựng từ A
→ Dựa vào đối xứng và song song, có thể suy ra AEAE chia đôi góc ∠HAC\angle HAC
AE laˋ phaˆn giaˊc của ∠HAC\boxed{AE \text{ là phân giác của } \angle HAC} 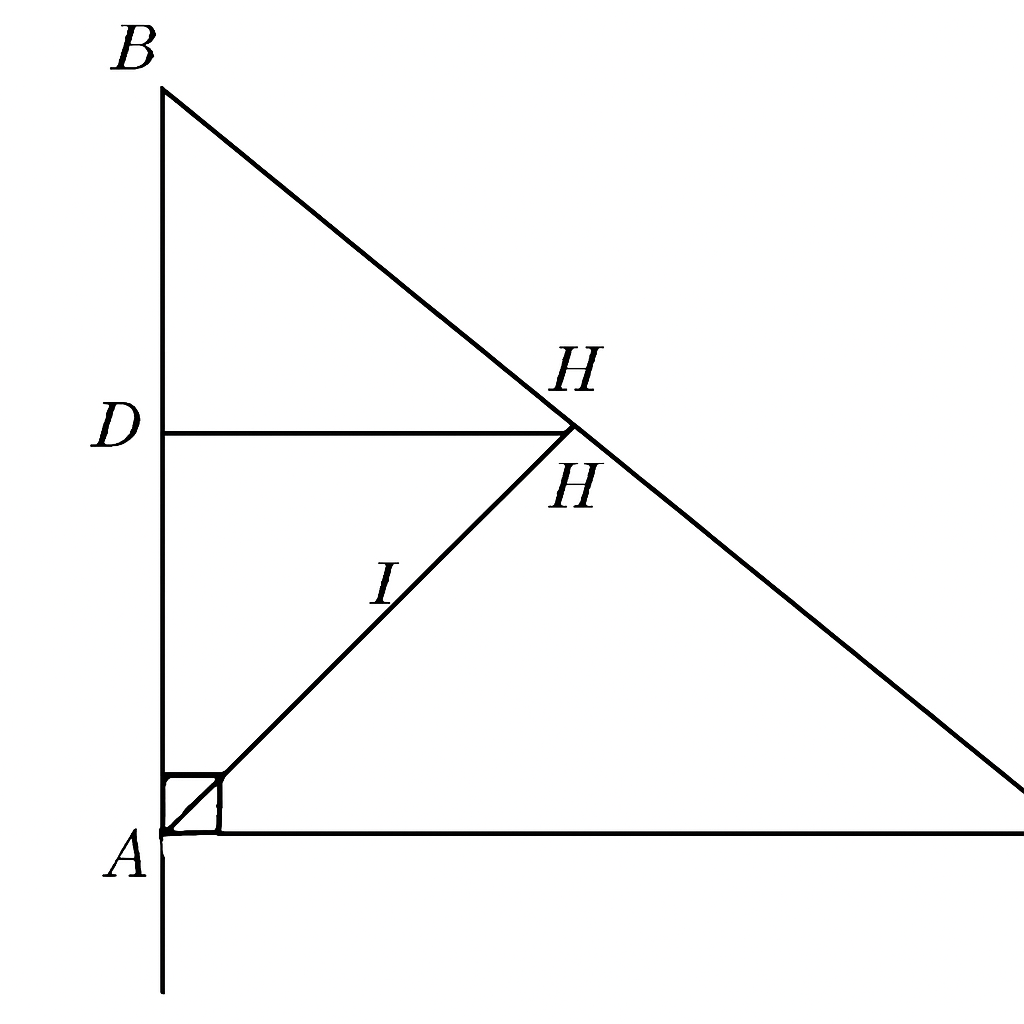
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515


