a) Chứng minh \( \triangle MHN \sim \triangle PHM \)

Xét 2 tam giác: \( \triangle MHN \) và \( \triangle PHM \)

Ta có:

- Cả hai đều vuông tại \( H \)
- Góc \( \angle MHN \) và \( \angle PHM \) đối đỉnh ⇒ bằng nhau

⇒ 2 tam giác có 1 góc vuông và 1 góc bằng nhau
→ \( \triangle MHN \sim \triangle PHM \) (g.g)

b) Tính \( MH, NH, HP \)

Áp dụng hệ thức trong tam giác vuông có đường cao:

Tam giác \( MNP \) vuông tại \( M \), \( MH \perp NP \)

Gọi các đoạn như sau:
- \( MN = 5 \)
- \( NP = \sqrt{41} \)
- \( MP = x \) ⇒ Ta tính \( x \) bằng định lý Pythagoras:
\[
MP^2 = NP^2 - MN^2 = 41 - 25 = 16 \Rightarrow MP = 4 \, \text{cm}
\]

1. Tính MH (đường cao)

Trong tam giác vuông có đường cao từ góc vuông:

\[
MH^2 = MN \cdot MP = 5 \cdot 4 = 20
\Rightarrow MH = \sqrt{20} = 2\sqrt{5} \, \text{cm}
\]

2. Tính NH và HP

Công thức:

\[
NH = \frac{MN^2}{NP} = \frac{25}{\sqrt{41}} = \frac{25\sqrt{41}}{41} \, \text{cm}
\]

\[
HP = \frac{MP^2}{NP} = \frac{16}{\sqrt{41}} = \frac{16\sqrt{41}}{41} \, \text{cm}
\]

 a) \( \triangle MHN \sim \triangle PHM \)
 b)
 \( MH = 2\sqrt{5} \, \text{cm} \)
 \( NH = \dfrac{25\sqrt{41}}{41} \, \text{cm} \)
\( HP = \dfrac{16\sqrt{41}}{41} \, \text{cm} \)

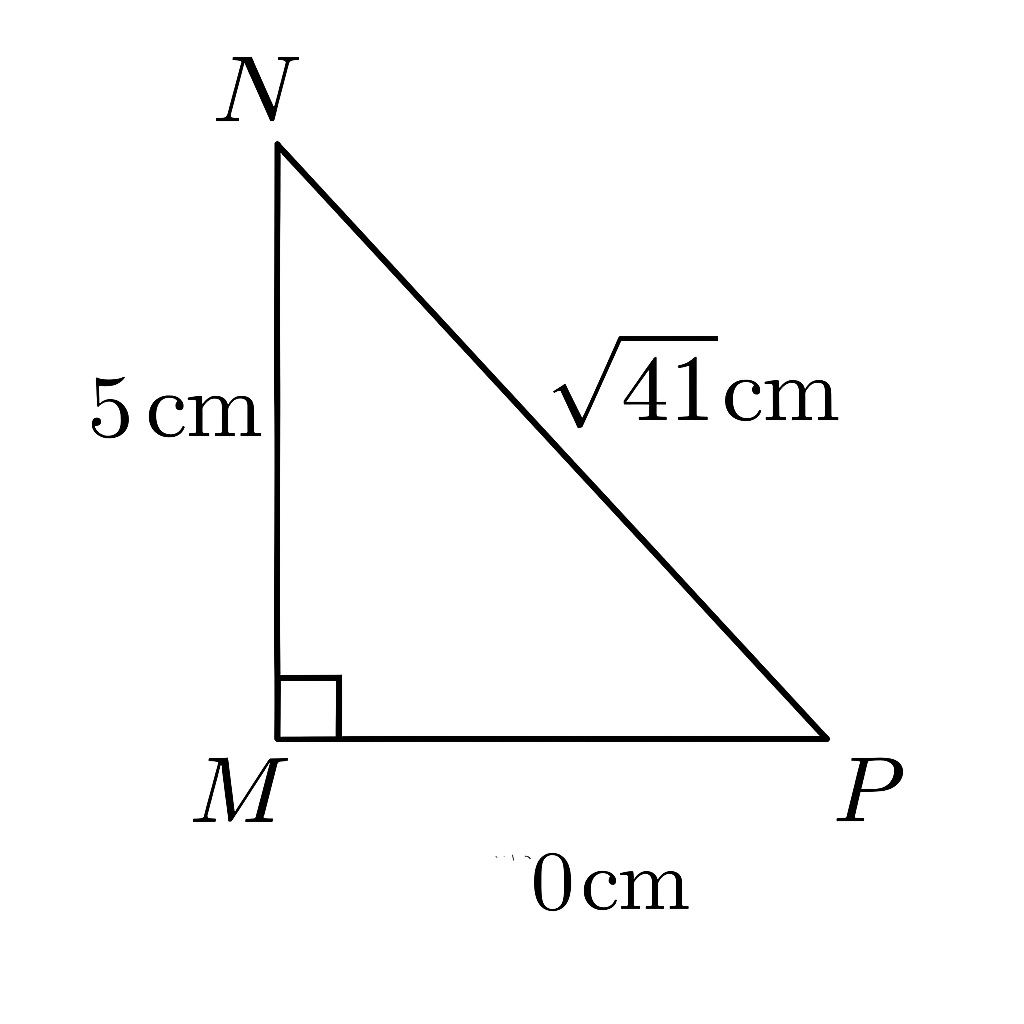
a) xét 2 tam giác MHN và PHM

Tam giác MNP vuông tại M => góc ∠MNP = 90 độ.
 Có góc ∠HMN chung.
 Trong tam giác MNP, ta có ∠MNP = 90 độ.

=> ∠HMN = ∠HMP (góc chung)
=> ∠MNP = 90 độ

=> Hai tam giác MHN và PHM có hai cặp góc tương ứng bằng nhau (góc chung và góc vuông).

 => Tam giác MHN đồng dạng với tam giác PHM (g.g)

 b) 

- Ta có tam giác MNP vuông tại M, áp dụng định lý Pythagore:
\[
MN^2 + MH^2 = NP^2
\]
- Thay số vào:
\[
5^2 + MH^2 = (\sqrt{41})^2
\]
\[
25 + MH^2 = 41
\]
\[
MH^2 = 41 - 25 = 16
\]
\[
MH = \sqrt{16} = 4 \text{ cm}
\]

- Trong tam giác MHP, áp dụng định lý Pythagore:
\[
HP^2 = MH^2 + NH^2
\]
\[
HP^2 = MN^2 + MH^2
\]
\[
HP = NP = \sqrt{41} \text{ cm}
\]
- Áp dụng định lý Pythagore cho tam giác MHP:
\[
NH^2 = HP^2 - MH^2
\]
\[
NH^2 = 41 - 16 = 25
\]
\[
NH = \sqrt{25} = 5 \text{ cm}
\]

- HP đã được tính ở trên, ta có:
\[
HP = \sqrt{41} \text{ cm}
\]

 Kết luận:
- \( MH = 4 \text{ cm} \)
- \( NH = 5 \text{ cm} \)
- \( HP = \sqrt{41} \text{ cm} \)