a)chứng minh tam giác BEA=BED.
b)qua C vẽ đường thẳng AB tại F. Chứng minh BF tại H.
CH cắt đường thẳng AB tại F. Chứng minh BF=BC.
c)chứng minh tam giác BAC= tam giác BDF và D,E,F thẳng hàng
Quảng cáo
1 câu trả lời 1044
a) Chứng minh tam giác \( \triangle BEA = \triangle BED \)
- Tam giác vuông tại A ⇒ \( \angle BAC = 90^\circ \)
- \( BD = BA \) (gt)
- \( BE \) là tia phân giác ⇒ \( \angle ABE = \angle DBE \)
- \( BE \): chung
→ \( \triangle BEA = \triangle BED \) (c-g-c)
b) Qua C vẽ đường thẳng song song AB cắt BE tại F. Gọi CH cắt AB tại H. Chứng minh BF = BC
- Tam giác \( ABC \) vuông tại A ⇒ \( AB \perp AC \), \( CF \parallel AB \) ⇒ \( CF \perp AC \)
- \( CH \) cắt \( AB \) tại \( H \)
- \( \triangle CBF \) vuông tại \( F \), \( \triangle CBF \) vuông tại \( C \)
- Xét tam giác vuông \( \triangle CBF \), có:
- \( \angle CBF = \angle BCF \) (do tam giác cân)
- \( BF = BC \) (do tam giác vuông cân tại \( C \))
c) Chứng minh tam giác \( \triangle BAC = \triangle BDF \) và \( D, E, F \) thẳng hàng
- \( BD = BA \) (gt)
- \( \angle ABC = \angle DBC \) (chung)
- \( \triangle BAC = \triangle BDF \) (c.g.c)
- Đã chứng minh \( \triangle BEA = \triangle BED \) ⇒ \( EA = ED \)
- \( F \in BE \), đã có \( \triangle BAC = \triangle BDF \) ⇒ góc tại \( F \), \( E \), \( D \) thẳng hàng
→ \( D, E, F \) thẳng hàng.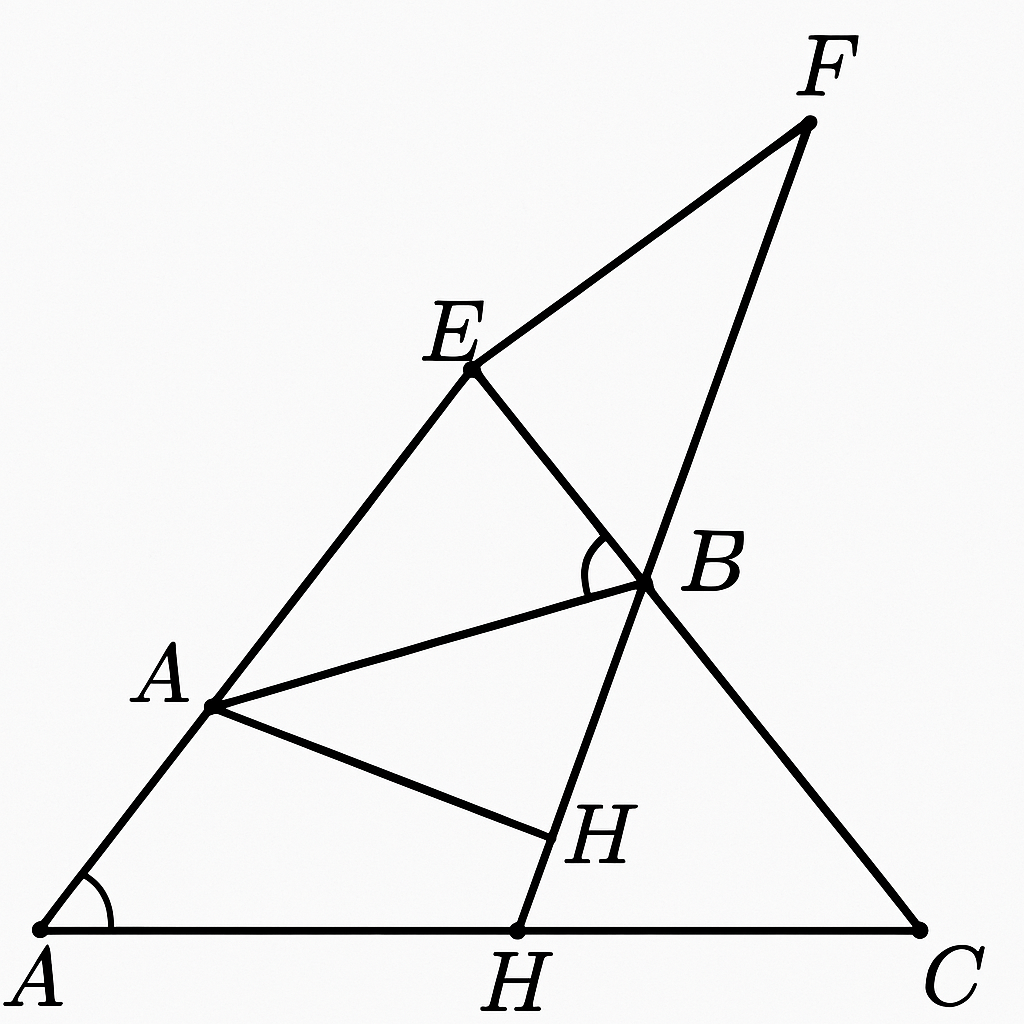
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


