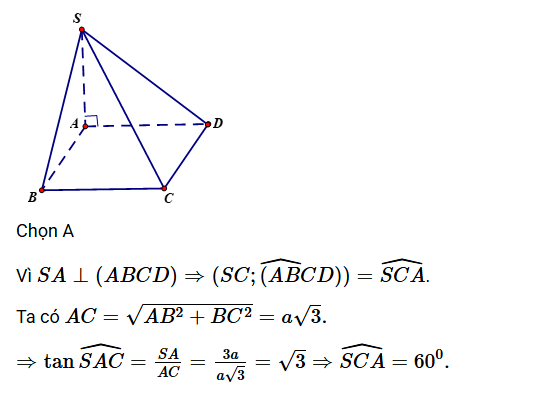
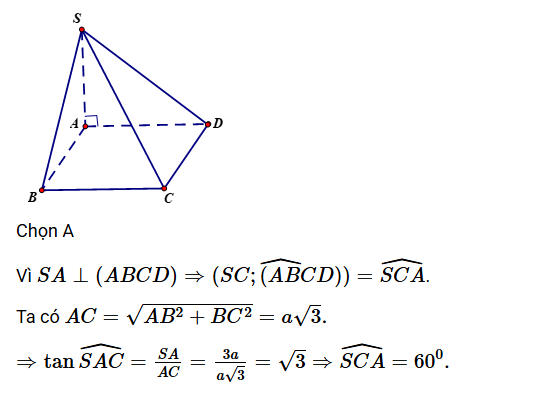
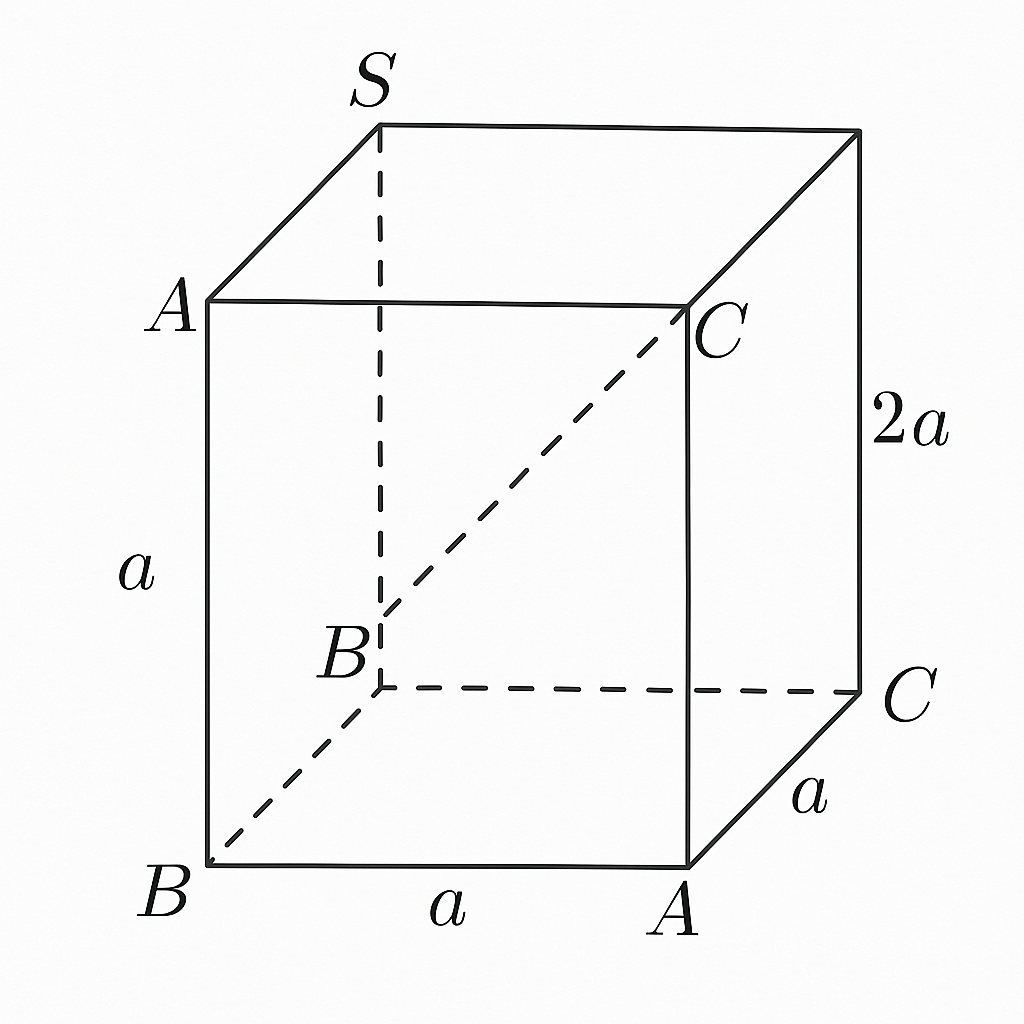
Tìm véc-tơ chỉ phương của đường thẳng SC

- \( S(0, 0, 3a) \), \( C(a, 2a, 0) \)

\[
\vec{SC} = \overrightarrow{C} - \overrightarrow{S} = (a, 2a, -3a)
\]

Viết véc-tơ từ điểm B đến đường thẳng SC

- \( B(a, 0, 0) \), \( S(0, 0, 3a) \)

\[
\vec{SB} = \overrightarrow{B} - \overrightarrow{S} = (a, 0, -3a)
\]

Tính khoảng cách từ điểm B đến đường thẳng SC

Ta dùng công thức khoảng cách từ điểm đến đường thẳng (dạng véc-tơ):

\[
\text{Khoảng cách} = \frac{|\vec{u} \times \vec{v}|}{|\vec{v}|}
\]

Trong đó:

- \( \vec{u} = \vec{SB} = (a, 0, -3a) \)
- \( \vec{v} = \vec{SC} = (a, 2a, -3a) \)

Tính tích có hướng \( \vec{SB} \times \vec{SC} \):

\[
\vec{SB} \times \vec{SC} =
\begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
a & 0 & -3a \\
a & 2a & -3a \\
\end{vmatrix}
= \mathbf{i}(0 \cdot (-3a) - (-3a)(2a))
- \mathbf{j}(a \cdot (-3a) - (-3a)(a))
+ \mathbf{k}(a \cdot 2a - 0 \cdot a)
\]

\[
= \mathbf{i}(6a^2) - \mathbf{j}( -3a^2 + 3a^2) + \mathbf{k}(2a^2)
= (6a^2, 0, 2a^2)
\]

⇒ \( |\vec{SB} \times \vec{SC}| = \sqrt{(6a^2)^2 + 0 + (2a^2)^2} = \sqrt{36a^4 + 4a^4} = \sqrt{40a^4} = a^2 \sqrt{40} \)

Tính độ dài \( |\vec{SC}| \):

\[
|\vec{SC}| = \sqrt{a^2 + (2a)^2 + (-3a)^2} = \sqrt{a^2 + 4a^2 + 9a^2} = \sqrt{14a^2} = a\sqrt{14}
\]

Kết quả:

\[
\text{Khoảng cách} = \frac{|\vec{SB} \times \vec{SC}|}{|\vec{SC}|} = \frac{a^2 \sqrt{40}}{a \sqrt{14}} = a \cdot \frac{\sqrt{40}}{\sqrt{14}} = a \cdot \sqrt{\frac{40}{14}} = a \cdot \sqrt{\frac{20}{7}}
\]

\[
\boxed{a \cdot \sqrt{\frac{20}{7}}}
\]