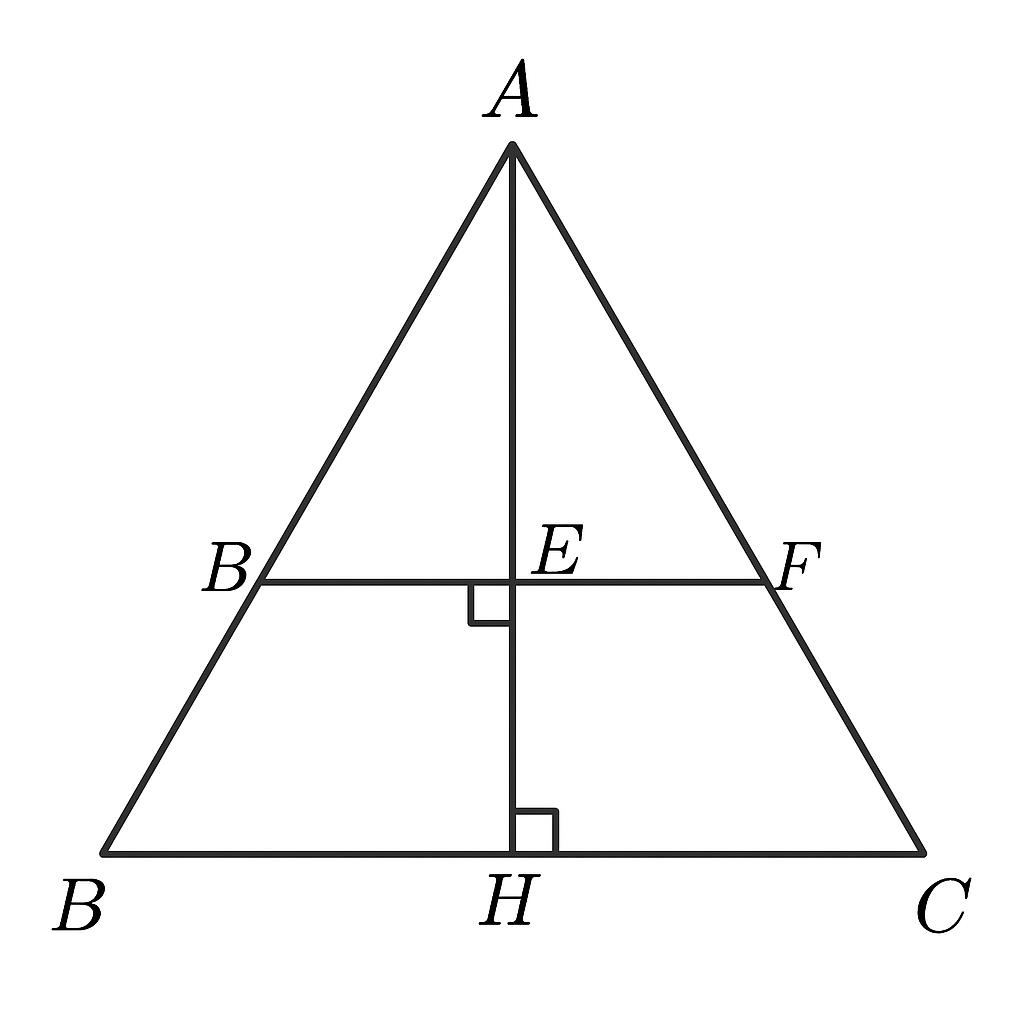
a) CM: tam giác AHB= Tg AHC
b) Qua điểm H, kẻ HE vuông góc AB(E thuộc AB) , HF vuông góc AC(F thuộc AC). CM: tg HEF cân.
Quảng cáo
1 câu trả lời 322
a) Chứng minh: \( \triangle AHB = \triangle AHC \)
Xét hai tam giác \( \triangle AHB \) và \( \triangle AHC \):
- \( AB = AC \) (tam giác cân tại A)
- \( BH = HC \) (H là trung điểm của BC)
- Chung cạnh: \( AH \)
→ Hai tam giác có: 3 cạnh tương ứng bằng nhau
\( \triangle AHB = \triangle AHC \) (c.c.c)
Đpcm
b) Qua điểm H, kẻ:
- \( HE \perp AB \) tại E
- \( HF \perp AC \) tại F
→ Chứng minh tam giác \( \triangle HEF \) cân
Phân tích:
Từ a) ta đã có:
- \( \triangle AHB = \triangle AHC \)
→ Hai tam giác vuông tại E và F sẽ đối xứng nhau qua đường trung tuyến AH (vì tam giác cân)
→ Suy ra:
- \( HE = HF \) (vì đối xứng)
- Góc \( \angle HEF = \angle HFE \) (vì hai tam giác vuông bằng nhau, tương ứng)
⇒ Kết luận:
- Tam giác \( \triangle HEF \) có:
+ Hai cạnh bằng nhau: \( HE = HF \)
+ Hai góc kề đáy bằng nhau
→ \( \triangle HEF \) cân tại H
Đpcm
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


