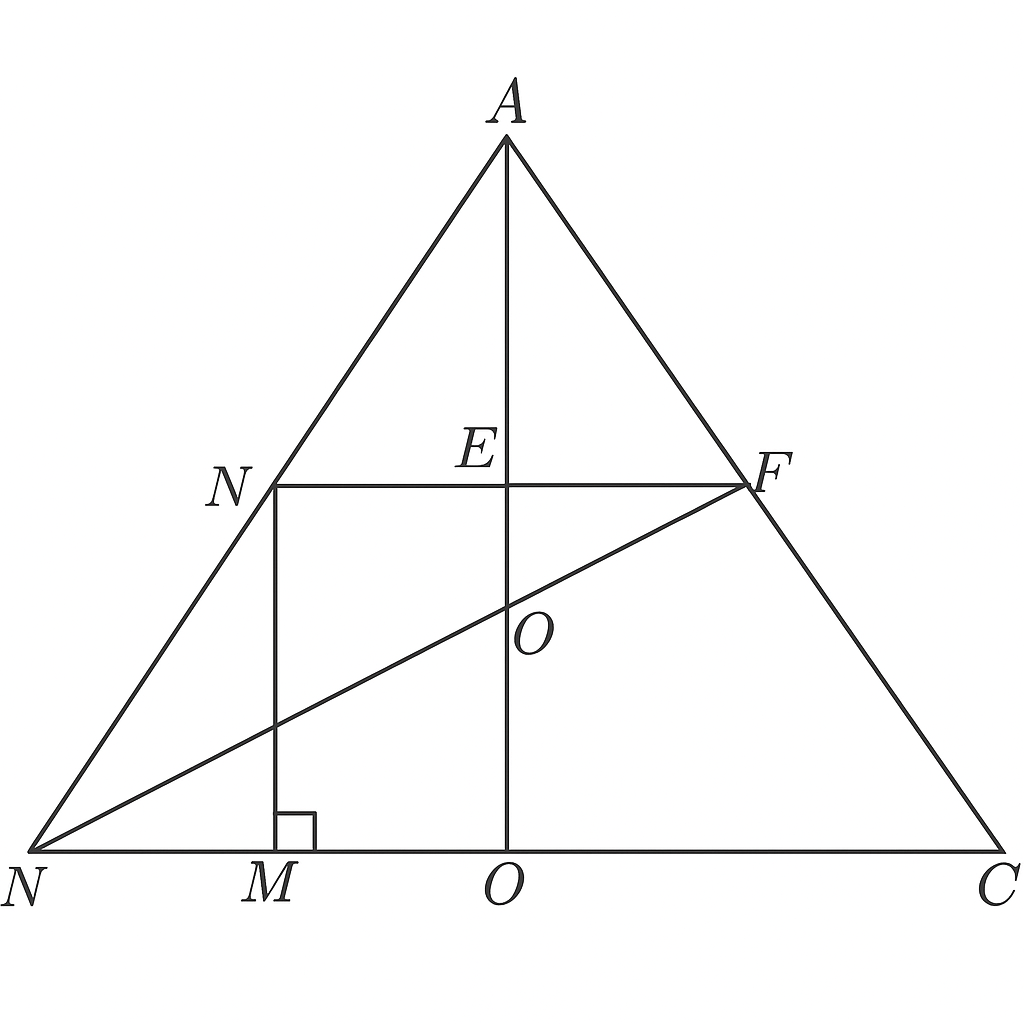
Cho tam giác ABC cân tại A . Lấy điểm M trên cạnh BC (MB MC). Trên tia
đối của tia CB lấy điểm N sao cho BM CN . Đường thẳng qua M vuông góc với
BC cắt AB tại E . Đường thẳng qua N vuông góc BC cắt AC tại F .
a) Chứng minh: EM FN
b) Qua E kẻ ED // AC ( D BC ). Chứng minh MB MD .
c) EF cắt BC tại O . Chứng minh OE OF
VẼ HỘ TỚ HÌNH NHA
Quảng cáo
2 câu trả lời 474
a) Chứng minh: \( EM = FN \)
Xét hai tam giác vuông:
- Tam giác \( \triangle EM B \) vuông tại \( M \)
- Tam giác \( \triangle FNC \) vuông tại \( N \)
Ta có:
- \( MB = CN \) (giả thiết)
- \( \angle EMB = \angle FNC = 90^\circ \)
- \( AB = AC \) (tam giác cân tại A)
⇒ Hai tam giác vuông \( \triangle EMB \) và \( \triangle FNC \) bằng nhau (cạnh huyền – góc vuông – cạnh góc vuông)
→ Suy ra: \( \boxed{EM = FN} \)
b) Qua E kẻ \( ED \parallel AC \), \( D \in BC \). Chứng minh \( MB = MD \)
Xét hai tam giác:
- \( \triangle EMB \) vuông tại M
- \( \triangle DMB \): có \( ED \parallel AC \)
⇒ Tam giác \( \triangle EMD \sim \triangle FAC \) (do đồng dạng tam giác, vì góc và song song)
Tuy nhiên cách dễ hơn:
- \( ED \parallel AC \), mà tam giác ABC cân tại A ⇒ trục đối xứng là phân giác và đường cao từ A
- Vì \( E \in AB \), và \( ED \parallel AC \), suy ra \( D \) là ảnh đối xứng của \( B \) qua đường trung trực BC (hoặc từ tính chất hình thang cân)
- Đồng thời, \( EM \perp BC \), nên \( M \) là chân đường cao từ \( E \), và \( MD \perp BC \)
⇒ Tam giác \( \triangle MBD \) có M là trung điểm của BD
Vì:
- \( \angle EMB = \angle DME \)
- \( BM = MD \)
→ \( \boxed{MB = MD} \)
c) EF cắt BC tại O. Chứng minh \( OE = OF \)
Ta đã có:
- \( EM = FN \) (câu a)
- \( EF \) là đoạn nối từ \( E \) đến \( F \)
- \( EM \perp BC \), \( FN \perp BC \) ⇒ \( EF \) vuông góc với BC tại O
⇒ O là hình chiếu vuông góc của cả \( E \) và \( F \) xuống BC ⇒ đoạn thẳng \( OE = OF \)
\[
\boxed{
\begin{aligned}
&\text{a) } EM = FN \\
&\text{b) } MB = MD \\
&\text{c) } OE = OF
\end{aligned}
}
\]
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


