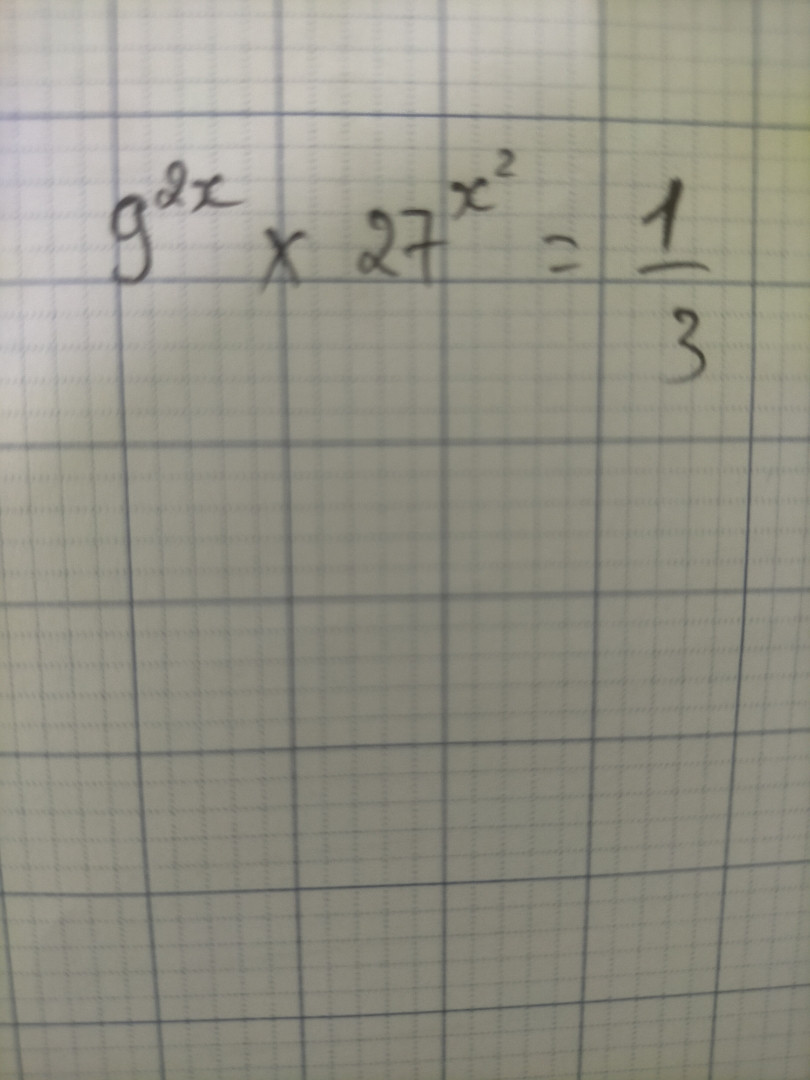Giải dạng bài phương trình mũ
Quảng cáo
2 câu trả lời 244
Để giải phương trình mũ \( 9 \cdot 2^x \cdot 27^{x^2} = \frac{1}{3} \), ta cần sử dụng các phương pháp biến đổi phương trình mũ. Dưới đây là cách giải chi tiết:
Đầu tiên, ta có thể viết lại phương trình dưới dạng các cơ số là 3:
\[ 9 = 3^2 \]
\[ 27 = 3^3 \]
Vậy phương trình sẽ trở thành:
\[ 3^2 \cdot 2^x \cdot (3^3)^{x^2} = \frac{1}{3} \]
Tiếp theo, ta biến đổi phương trình:
\[ 3^2 \cdot 2^x \cdot 3^{3x^2} = 3^{-1} \]
Kết hợp các lũy thừa của 3:
\[ 3^{2 + 3x^2} \cdot 2^x = 3^{-1} \]
Chia hai vế cho \( 3^{2 + 3x^2} \):
\[ 2^x = 3^{-1 - (2 + 3x^2)} \]
\[ 2^x = 3^{-(3x^2 + 3)} \]
Để giải phương trình này, ta cần so sánh cơ số của hai vế, tuy nhiên \( 2 \) và \( 3 \) không có cơ số chung, nên ta cần xem xét các giá trị của \( x \).
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
zytera
1325 điểm
-
Dương Nguyễn
960 điểm
-
보고 싶어요
855 điểm
-
돈이없다 💸😭
815 điểm
-
우옌 ✨
790 điểm
-
`d.`
635 điểm
-
`color{blue}text{HuyTùng.`
555 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
540 điểm
-
주디 홉스닉주디🥵👍
520 điểm
-
‧₊˚✩ ₊˚🎧⊹♡≽☁˚˖ִ໋🌷͙֒✧˚.🎀༘⋆⋅♡👾đẹρ-†®åî⋆⭒💫
435 điểm
-
Ngọc Linh hay nói linh tinh
385 điểm
-
Kiều Anh 350 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
345 điểm
-
Bích Hồng 345 điểm
Rút gọn
Bài viết mới nhất Lớp 11
-
3 năm trước3540
-
3 năm trước3381
