2. Phân tích bài toán
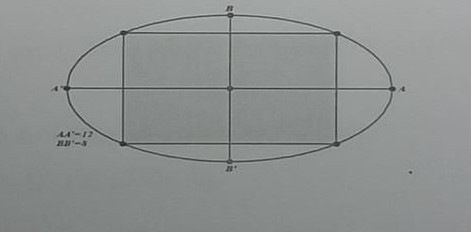
Gọi: a = 6 (m): Nửa trục lớn của elip.
b = 4 (m): Nửa trục bé của elip.
x, y (m): Nửa chiều dài và nửa chiều rộng của hình chữ nhật nội tiếp.
Diện tích hình chữ nhật: S = 4xy.
Phương trình elip: Với tâm O, trục lớn trùng với trục Ox, ta có phương trình: (x²/a²) + (y²/b²) = 1.
3. Giải bài toán
Mối liên hệ giữa x và y: Vì một đỉnh của hình chữ nhật nằm trên elip, ta có: (x²/36) + (y²/16) = 1. Từ đó suy ra: y² = 16(1 - x²/36) = (16/9)(36 - x²).
Biểu diễn diện tích S theo x: S = 4xy = 4x * √[(16/9)(36 - x²)] = (16/3)x√(36 - x²).
Tìm giá trị lớn nhất của S: Để tìm diện tích lớn nhất, ta có thể sử dụng đạo hàm:Tính đạo hàm của S theo x: S'(x) = (16/3)[√(36 - x²) - (x²/√(36 - x²))]
Giải phương trình S'(x) = 0: (16/3)[√(36 - x²) - (x²/√(36 - x²))] = 0 ⇔ √(36 - x²) - (x²/√(36 - x²)) = 0 ⇔ 36 - x² - x² = 0 ⇔ 2x² = 36 ⇔ x² = 18 ⇔ x = 3√2 (vì x > 0)
Thay x = 3√2 vào biểu thức S, ta được Smax = (16/3) * 3√2 * √(36 - 18) = 32√2 (m²)
4. Kết luận
Diện tích trồng hoa lớn nhất là 32√2 m².

Vậy, diện tích trồng hoa lớn nhất có thể đạt được là 32√2 mét vuông.