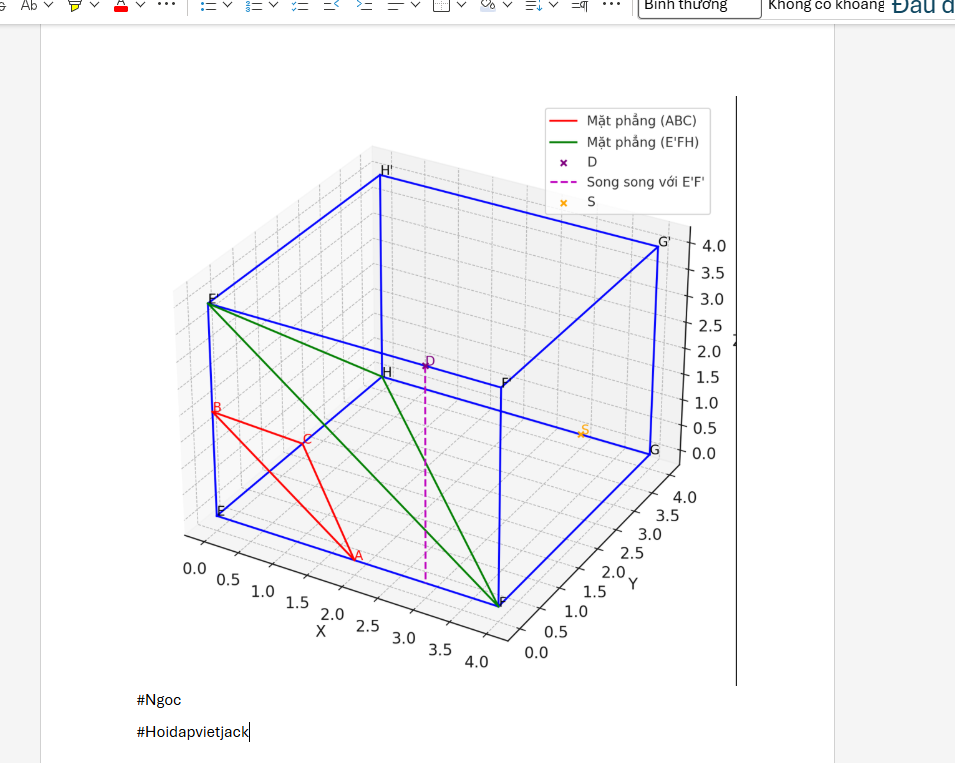
a) Chứng minh rằng (ABC) // (E'FH)

xd các vectơ:

Ta có A, B, C lần lượt là trung điểm của EF, EE', EH.
Do đó:vec(EA) = 1/2 vec(EF)
vec(EB) = 1/2 vec(EE')
vec(EC) = 1/2 vec(EH)
Xác định các vectơ chỉ phương của mặt phẳng (ABC):

vec(AB) = vec(EB) - vec(EA) = 1/2 vec(EE') - 1/2 vec(EF) = 1/2 (vec(EE') - vec(EF))
vec(AC) = vec(EC) - vec(EA) = 1/2 vec(EH) - 1/2 vec(EF) = 1/2 (vec(EH) - vec(EF))
Xác định các vectơ chỉ phương của mặt phẳng (E'FH):

vec(E'F) = vec(EF) (Vì EFGH.E'F'G'H' là hình hộp chữ nhật nên EF // E'F)
vec(FH) = vec(EH) - vec(EF)
CM  hai mặt phẳng //

Ta thấy vec(AB) và vec(AC) là tổ hợp tuyến tính của vec(E'F) và vec(FH).
Cụ thể:vec(AB) = 1/2 (vec(EE') - vec(EF)) = -1/2 vec(E'F) + 1/2 vec(EE')
vec(AC) = 1/2 (vec(EH) - vec(EF)) = -1/2 vec(E'F) + 1/2 vec(FH)
Mặt khác, vì EE'//(E'FH) , vec(EE') không cùng phương với vec(E'F) và vec(FH)
Do đó, vec(AB) và vec(AC) không cùng phương.
Hơn nữa, ta thấy vec(AB) và vec(AC) lần lượt song song hoặc nằm trên mặt phẳng (E'FH) (vì chúng là tổ hợp tuyến tính của hai vectơ chỉ phương của mặt phẳng (E'FH)).
=> Kết luận: Hai mặt phẳng (ABC) và (E'FH) có hai cặp vectơ chỉ phương không cùng phương và lần lượt song song hoặc trùng nhau, do đó (ABC) // (E'FH).

b) Tính (SG)/(SG')

Xác định giao tuyến:

Mặt phẳng (α) song song với (EFGH) nên giao tuyến của (α) và (E'F'G'H') là đường thẳng d đi qua D và song song với E'F'.
Xác định vị trí của S:

Vì S thuộc GG' và S thuộc (α) nên S thuộc giao tuyến của (α) và mặt phẳng (E'F'G'G).
Mặt khác, giao tuyến của (α) và (E'F'G'G) là đường thẳng đi qua D và song song với E'G'.
Do đó, S là giao điểm của GG' và đường thẳng đi qua D song song với E'G'.
Sử dụng định lý Thales:

Xét tam giác E'F'G' có DS // E'G'.
Theo định lý Thales, ta có:(E'D)/(E'F') = (G'S)/(G'G)
Mà (E'D)/(E'F') = (E'D)/(EF) = 3/4 (vì E'F' = EF) và G'G = GG'
Suy ra (G'S)/(GG') = 3/4
Từ đó (SG')/(GG') = 3/4
Do đó (SG)/(GG') = 1/4
Vậy (SG)/(SG') = 1/3
=> Kết luận: (SG)/(SG') = 1/3