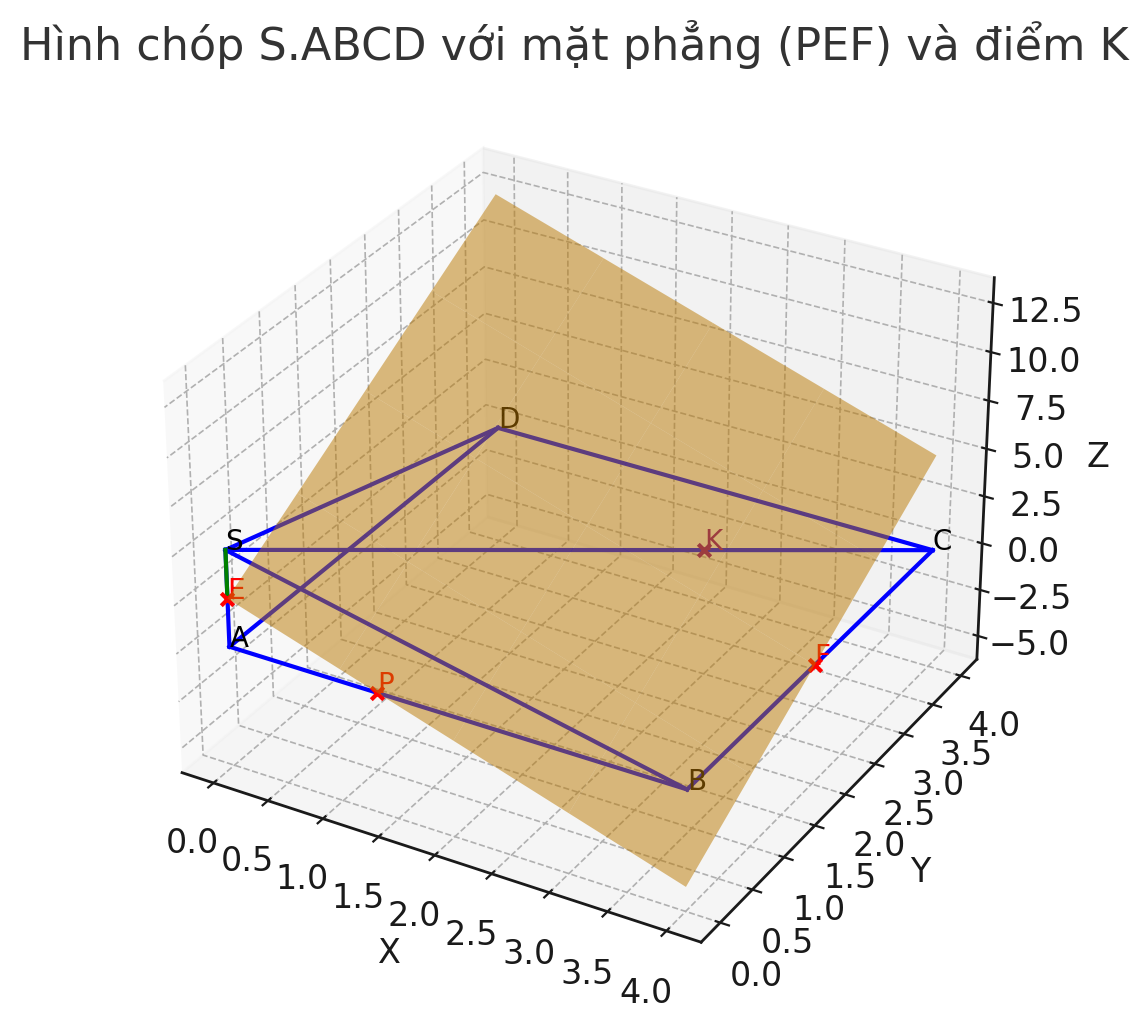
Cho hình chóp S.ABCD. Gọi E, F lần lượt là trung điểm SA và BC. P là điểm nằm trên cạnh AB sao cho . Gọi K là giao điểm của SC và mặt phẳng (PEF). Tính (không dùng định lý Menelaus)
Quảng cáo
1 câu trả lời 110
Gọi I là giao điểm của PF và AC.
Trong mặt phẳng (ABC), gọi J là giao điểm của EF và AC.
Ta có:
E là trung điểm của SA.
F là trung điểm của BC.
Cho tỉ số:
AP / AB = 1 / 3
PB / AB = 2 / 3
Áp dụng định lý Ta-let:
Trong tam giác ABC, PF cắt AC tại I:
AI / IC = AP / PB = 1 / 2
AB / BC = 1 / 3
=> IC = 3AI
Trong tam giác SAC, EF // AC:
AJ / JC = AE / ES = 1 => AJ = JC
Suy ra: AC = 4AI = 2AJ
=> AJ = 2AI = JC
=> AI = IJ = JC
Trong mặt phẳng (SAC), gọi K là giao điểm của El và SC.
Áp dụng định lý Ta-let cho tam giác SIC:
Tam giác SKC có EK / IC = SK / KC
Tam giác SJC có EK / JC = SJ / JC
Tam giác SJC có EK / JC = 1 / 2
SI / SC = EI / IC = SE / IA = 1 / 2
SK / KC = SI / IC = 1 / 2
EI / IJ = SE / EA = 1
=> SK / KC = 2 / 3
=> KC = 2SK
SC = SK + KC = 3SK
=> SK / SC = 1 / 3
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
134901
Đã trả lời bởi chuyên gia
134901 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
76057
Đã trả lời bởi chuyên gia
76057 -
 Đã trả lời bởi chuyên gia
71711
Đã trả lời bởi chuyên gia
71711 -
 Đã trả lời bởi chuyên gia
47598
Đã trả lời bởi chuyên gia
47598


