Bài 1. Cho hai hình binh hành ABCD và ABEF không cùng năm trong một mặt phăng. Goi O và O' lân lượt là tâm của hai hinh bình hành ABCD và ABEF. a. Chứng minh O O' song song với các mặt phăng (ADF) và (BCE). b. Goi G và G' làn lượt là trọng tâm các tam giác ABD và ABF. Chứng minh GG'// (DCEF)
Quảng cáo
1 câu trả lời 302
a) Do các tứ giác ABCD và ABEF là các hình bình hành
$\Rightarrow$ O là trung điểm của AC và BD
và O’ là trung điểm của AE và BF. (tính chất hình bình hành).
+ ΔBFD có OO’ là đường trung bình nên OO’ // DF mà DF ⊂ (ADF)
$\Rightarrow$ OO' // (ADF)
+ ΔAEC có OO’ là đường trung bình nên OO’ // EC mà EC ⊂ (BCE)
$\Rightarrow$ OO’ // (BCE).
b)
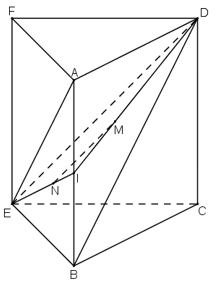
Ta thấy mp(CEF) chính là mp(CEFD).
Gọi I là trung điểm của AB:
+ M là trọng tâm ΔABD
$\Rightarrow$ IM/ ID = 1/3.
+ N là trọng tâm ΔABE
$\Rightarrow$ IN/IE = 1/3.
+ ΔIDE có IM/ID = IN/IE = 1/3
$\Rightarrow$ MN // DE mà ED ⊂ (CEFD)
nên MN // (CEFD) hay MN // (CEF).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
135031
Đã trả lời bởi chuyên gia
135031 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
76320
Đã trả lời bởi chuyên gia
76320 -
 Đã trả lời bởi chuyên gia
71863
Đã trả lời bởi chuyên gia
71863 -
 Đã trả lời bởi chuyên gia
47639
Đã trả lời bởi chuyên gia
47639
Gửi báo cáo thành công!


