Cho tam giác ABC có các góc nhọn nhỏ hơn 12001200. Vẽ ở phía ngoài tam giác ABC các tam giác đều ABD, ACE. Gọi M là giao điểm của DC và BE. Chứng minh rằng:
a) BMCˆBMC^=120 120
b) AMBˆAMB^=120
Quảng cáo
1 câu trả lời 845
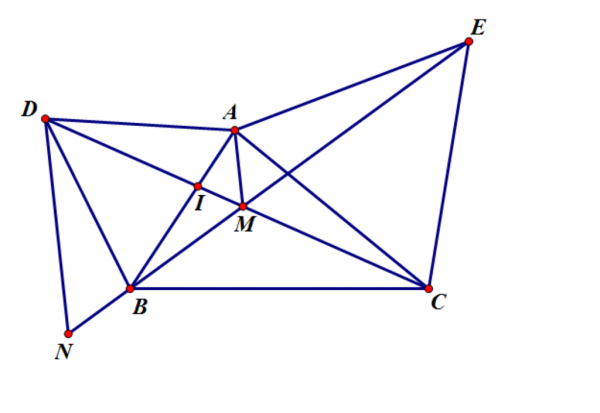
a,
Xét 2 tam giác EAB và CAD có:
AB = AD; ; AE = AC
=> 2 tam giác bằng nhau (c,g,c)
=>
Xét 2 tam giác ADI và MBI có:
=>
b,
Từ M kẻ MN = MD;
=> DMN là tam giác đều
xét 2 tam giác ADM và BDN có:
AD = DB; ; DM = DN;
=> 2 tam giác bằng nhau (c, g,c )
=>
=> (dpcm)
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757
Gửi báo cáo thành công!


