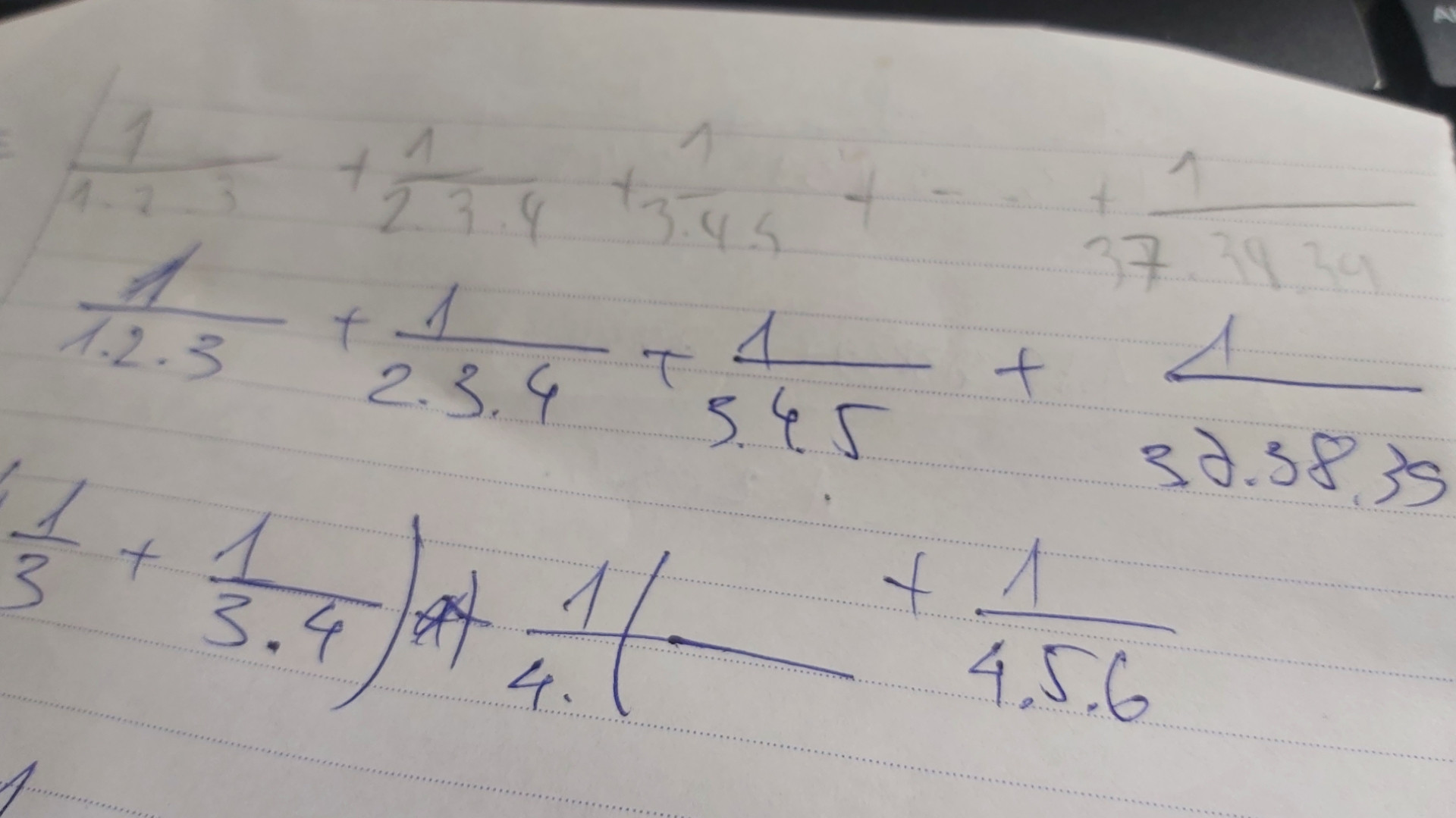Để giải bài toán \( \frac{1}{1 \times 2 \times 3} + \frac{1}{2 \times 3 \times 4} + \frac{1}{3 \times 4 \times 5} + \cdots + \frac{1}{37 \times 38 \times 39} \), ta có thể sử dụng phương pháp phân tích phân số thành các phân số đơn giản hơn.

Ta sẽ chứng minh rằng tổng của dãy số này có dạng như sau:

\[ S = \sum_{n=1}^{37} \frac{1}{n(n+1)(n+2)} \]

### Bước 1: Phân Tích Phân Số

Phân số \(\frac{1}{n(n+1)(n+2)}\) có thể được phân tích thành các phân số đơn giản hơn. Ta sử dụng phương pháp phân số thành phần:

\[ \frac{1}{n(n+1)(n+2)} = \frac{A}{n} + \frac{B}{n+1} + \frac{C}{n+2} \]

Để tìm các hệ số \( A \), \( B \), và \( C \), ta nhân hai vế với \( n(n+1)(n+2) \) và so sánh các hệ số:

\[ 1 = A(n+1)(n+2) + Bn(n+2) + Cn(n+1) \]

Phân tích từng hệ số ta có:

1. **Khi \( n = 0 \):**
\[ 1 = A \times 1 \times 2 \]
\[ A = \frac{1}{2} \]

2. **Khi \( n = -1 \):**
\[ 1 = B \times (-1) \times 1 \]
\[ B = -1 \]

3. **Khi \( n = -2 \):**
\[ 1 = C \times (-2) \times (-1) \]
\[ C = \frac{1}{2} \]

Vậy:

\[ \frac{1}{n(n+1)(n+2)} = \frac{1/2}{n} - \frac{1}{n+1} + \frac{1/2}{n+2} \]

### Bước 2: Tính Tổng

Áp dụng phân tích trên vào tổng:

\[ S = \sum_{n=1}^{37} \left( \frac{1/2}{n} - \frac{1}{n+1} + \frac{1/2}{n+2} \right) \]

Khi tính tổng, ta có thể thấy rằng nhiều hạng tử sẽ bị triệt tiêu, chỉ còn lại một số hạng tử đầu và cuối. Cụ thể:

\[
\begin{aligned}
S &= \left( \frac{1/2}{1} - \frac{1}{2} + \frac{1/2}{3} \right) + \left( \frac{1/2}{2} - \frac{1}{3} + \frac{1/2}{4} \right) + \cdots + \left( \frac{1/2}{37} - \frac{1}{38} + \frac{1/2}{39} \right) \\
&= \frac{1/2}{1} + \frac{1/2}{2} - \frac{1}{38} + \frac{1/2}{39}
\end{aligned}
\]

Tính giá trị cụ thể:

\[
\begin{aligned}
S &= \frac{1/2}{1} + \frac{1/2}{2} - \frac{1}{38} + \frac{1/2}{39} \\
&= \frac{1}{2} + \frac{1}{4} - \frac{1}{38} + \frac{1}{78} \\
&= \frac{3}{4} - \frac{1}{38} + \frac{1}{78}
\end{aligned}
\]

Cuối cùng:

\[
S \approx \frac{3}{4} - \frac{1}{38} + \frac{1}{78} \approx 0.75 - 0.0263 + 0.0128 \approx 0.7365
\]

Do đó, tổng của dãy số này là \(\boxed{0.7365}\) (hoặc có thể biểu diễn dưới dạng phân số chính xác hơn tùy vào yêu cầu).