a,CM tam tam giác IMN=tam giác IKN
b,CM IK<IQ
c,CM NI đi qua trung điểm của đoạn thẳng PQ
Nhớ có hình nhé
Cảm ơn
Quảng cáo
2 câu trả lời 323
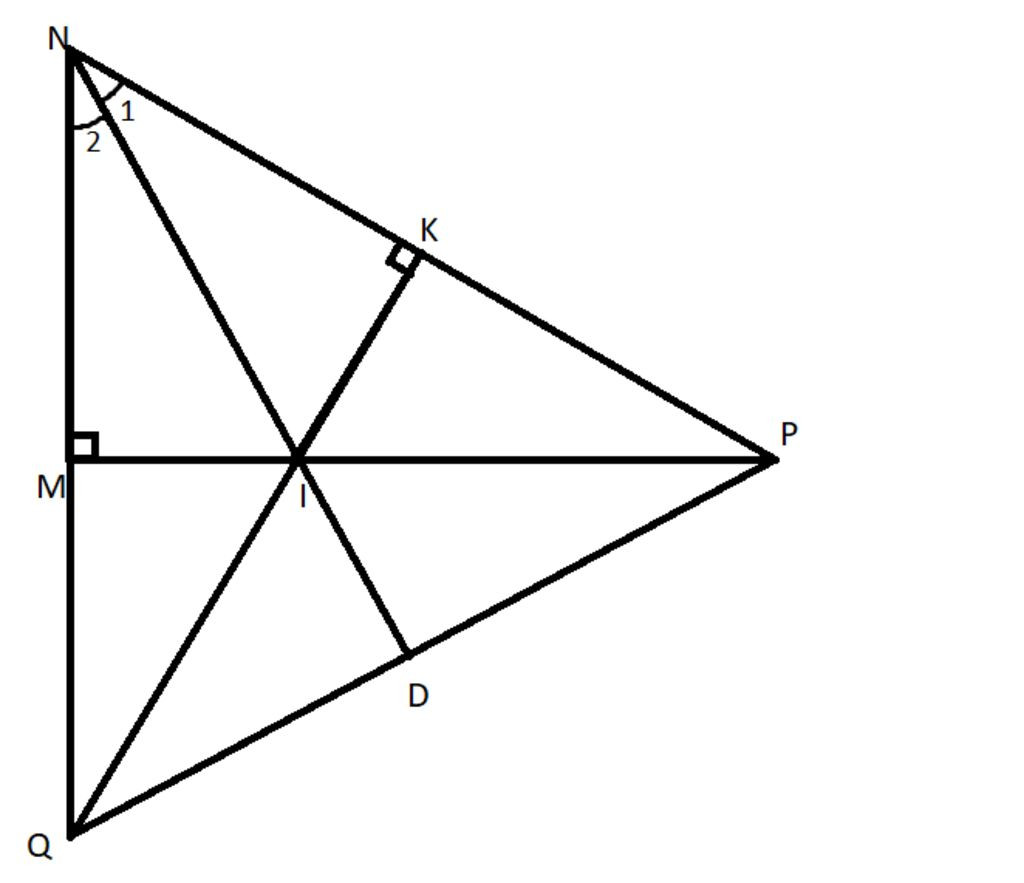
a) Ta có: ∠IMN=∠KIM (vì IK⊥NP), ∠MIN=∠KMI (vì MN là đường phân giác của∠MNP). Vậy IMN=IKM (cùng có hai góc bằng nhau và cạnh chung IM).
b) Ta có =90∠INK=∠IMP=90, do đó IN2=IP⋅IK. Cộng thêm 2IM2 vào hai vế ta được:
2IN2+IM2=IP⋅IK+IM2⇔MN2=IP⋅IK+MP2
Do MN<MP, suy ra 0IP⋅IK>0. Từ đó ta có 2MP2−MN2<IP⋅IK⇔MI2<IP2, hay MI<IP.
c) Ta có ∠IQP=∠INK=90−∠NIK=∠IKN=∠IQP, do đó tam giác QIP là tam giác cân tại I. Gọi E là hình chiếu vuông góc của D trên NP. Ta cần chứng minh NE⊥QP. Ta có DNI∼NKI, suy ra NKDN=KIDI=KPDP (vì DIP∼KIP). Từ đó:
DN=KPNK⋅DP
Gọi F là hình chiếu vuông góc của I lênMN. Ta có IMN=IKM nên FN=FK, suy ra NK=NP−PK=MN+MP−KP. Thay vào công thức trên ta được:
DN=KP(MN+MP−KP)⋅DP=KPMP⋅DP+MN−MP=KPIP⋅MK+MN−MP=KPIP⋅(MN+MP−NK)+MN−MP=KPIP⋅(MN+MP−MN−MP+KP)+MN−MP=IP−KPIP⋅KP+MN−MP=IP−IK+MN−MP=IN−IP
Do đó NE⊥QP (vì IN=IQ và IQP là tam giác cân tại I).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK121162
-
 Đã trả lời bởi chuyên gia
81971
Đã trả lời bởi chuyên gia
81971 -
 Đã trả lời bởi chuyên gia
59862
Đã trả lời bởi chuyên gia
59862 -
 Đã trả lời bởi chuyên gia
39757
Đã trả lời bởi chuyên gia
39757


