Cho tam giác ABC không phải là tam giác vuông, có các đường cao BE, CF cắt nhau tại điểm H.
a) Giả sử ABC là tam giác nhọn. Chứng minh rằng ∆ABE ᔕ ∆ACF; từ đó suy ra ∆AEF ᔕ ∆ABC. Kết quả đó còn đúng không, nếu ABC là tam giác tù (chỉ cần xét 2 trường hợp: góc A tù và góc B tù)?
c) Cho biết AB = 10 cm, BC = 15 cm và BE = 8 cm. Tính EF.
Quảng cáo
1 câu trả lời 76
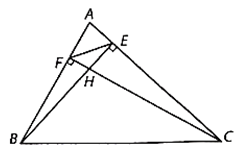
a) Khi tam giác ABC nhọn ta có hình bên.
Xét tam giác vuông ABE (vuông tại E) và tam giác vuông ACF (vuông tại F) có góc A chung nên ∆ABE ᔕ ∆ACF. Suy ra \[\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}.\]
Xét tam giác AEF và tam giác ABC có \(\widehat A\) chung và \(\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}\) nên ∆AEF ᔕ ∆ABC (c.g.c).
Khi tam giác ABC là tam giác tù, chẳng hạn góc A tù hoặc góc B tù, tương ứng ta có hai hình sau (HS tự vẽ):
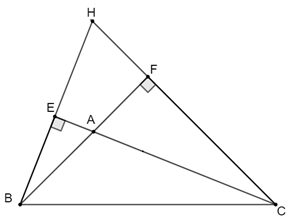
Trường hợp góc A tù
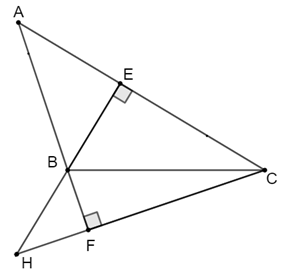
Trường hợp góc B tù
Chứng minh tương tự, ta thấy kết quả vẫn đúng.
b) Theo định lí Pythagore, trong tam giác ABE vuông tại E, ta có:
AB2 = AE2 + BE2
AE2 = AB2 – BE2
AE2 = 102 – 82 = 36 = 62
Suy ra AE = 6 cm.
Theo kết quả câu a), ta có:
∆AEF ᔕ ∆ABC suy ra \(\frac{{EF}}{{AE}} = \frac{{BC}}{{AB}}\) hay \(EF = \frac{{BC.AE}}{{AB}} = \frac{{15.6}}{{10}} = 9\) (cm).
Trả lời: EF = 9 cm.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


