Cho tam giác ABC cân tại đỉnh A. Hai đường phân giác BE và CF của tam giác ABC cắt nhau tại điểm I.
a) Chứng minh ∆BIC ᔕ ∆EIF.
b) Chứng minh FB2 = FI.FC.
c) Cho biết AB = 6 cm, BC = 3 cm. Tính EF.
Quảng cáo
1 câu trả lời 155
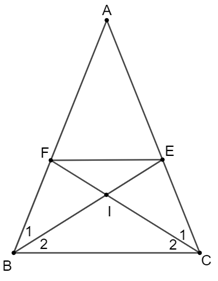
a) Do BE là đường phân giác của góc B nên \({\widehat B_1} = {\widehat B_2},\) ta có: \(\frac{{EA}}{{EC}} = \frac{{BA}}{{BC}}\) (1).
Tương tự với đường phân giác CF, ta có: \(\frac{{FA}}{{FB}} = \frac{{CA}}{{CB}}.\) (2)
Bởi vậy, từ (1) và (2) ta suy ra \(\frac{{EA}}{{EC}} = \frac{{FA}}{{FB}},\) nghĩa là EF định ra trên hai cạnh AB và AC những đoạn thẳng tương ứng tỉ lệ. Do đó theo định lí Thàles đảo ta có EF // BC. Từ đó suy ra ∆BIC ᔕ ∆EIF (ĐPCM).
b) Hai tam giác BFI và CFB có \(\widehat F\) chung, \({\widehat B_1} = \frac{{\widehat {ABC}}}{2} = \frac{{\widehat {ACB}}}{2} = \widehat C{ & _2}.\) Do đó ∆BFI ᔕ ∆CFB suy ra \(\frac{{FB}}{{FC}} = \frac{{FI}}{{FB}}\) hay FB2 = FI.FC (ĐPCM).
c) Ta có EF // BC (chứng minh trên).
Do đó \(\frac{{BC}}{{EF}} = \frac{{AB}}{{AF}} = \frac{{\left( {AF + FB} \right)}}{{AF}} = 1 + \frac{{BC}}{{AC}} = 1 + \frac{3}{6} = \frac{3}{2}.\)
Từ đó suy ra \(EF = 3:\frac{3}{2} = 2\) (cm).
Vậy EF = 2 cm.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


