Với giá trị nào của m, đường thẳng y = mx + 1 (m ≠ 0):
a) song song với đường thẳng y = 3x?
b) cắt trục hoành tại điểm có hoành độ bằng −2?
c) đồng quy với các đường thẳng y = 5x − 2 và y = −x + 4 (tức là ba đường thẳng này cắt nhau tại một điểm)? Với giá trị m tìm được, hãy vẽ ba đường thẳng này trên cùng một hệ trục tọa độ để kiểm nghiệm lại kết quả.
Quảng cáo
1 câu trả lời 131
a) Đường thẳng y = mx + 1 song song với đường thẳng y = 3x khi hai đường thẳng có cùng hệ số góc, tức là khi m = 3.
b) Đường thẳng y = mx + 1 cắt trục hoành có hoành độ bằng −2, tức là nó đi qua điểm (−2; 0). Điều đó xảy ra khi m.(−2) + 1 = 0, tức là \(m = \frac{1}{2}.\)
c) • Trước hết tìm giao điểm của hai đường thẳng y = 5x – 2 và y = −x + 4. Vẽ hai đường thẳng ấy trên cùng một hệ tọa độ (HS tự vẽ):
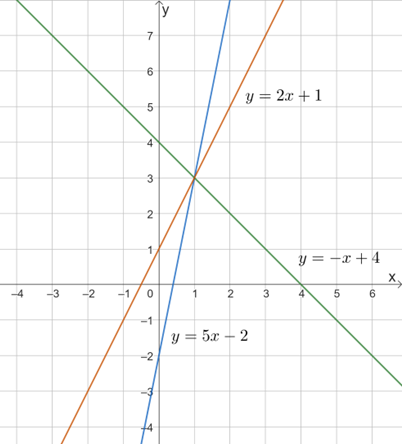
Trên hình vẽ ta thấy hai đường thẳng cắt nhau tại điểm (1; 3).
• Đường thẳng y = mx + 1 đi qua điểm (1; 3) nếu 3 = m + 1. Từ đó suy ra m = 2.
Vậy khi m = 2 thì ba đường thẳng đã cho đồng quy tại điểm (1; 3).
• Với m = 2, đồ thị của ba hàm số là ba đường thẳng như hình bên (HS tự vẽ).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


