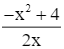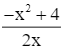Quảng cáo
1 câu trả lời 55
1) Tập xác định: D = ℝ\{0}.
2) Sự biến thiên
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
Ta có: ![]() y = −∞,
y = −∞, ![]() y = +∞.
y = +∞.
Do đó, hàm số không có đường tiệm cận ngang.
![]() y = −∞,
y = −∞, ![]() y = +∞.
y = +∞.
Do đó, đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số.
![]()
![]() =
= ![]()
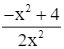 =
= ![]() .
.
![]()
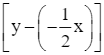 =
= ![]()
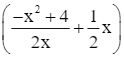 =
= ![]()
![]() = 0.
= 0.
Do đó, đường thẳng y = ![]() là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số.
Ta có y' = 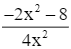 < 0 với ∀x ∈ D.
< 0 với ∀x ∈ D.
Ta có bảng biến thiên như sau:
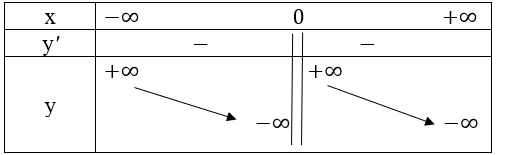
Hàm số nghịch biến trên các khoảng (−∞; 0) và (0; +∞).
Hàm số không có cực trị.
3) Đồ thị
Đồ thị nhận được thẳng x = 0 làm tiệm cận đứng, y = ![]() x làm tiệm cận xiên.
x làm tiệm cận xiên.
Đồ thị hàm số đi qua các điểm: 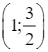 ;
; 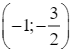 ;(2; 0);
;(2; 0); 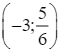 ; (−2; 0);
; (−2; 0); 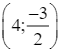 .
.
Có đồ thị hàm số như sau:
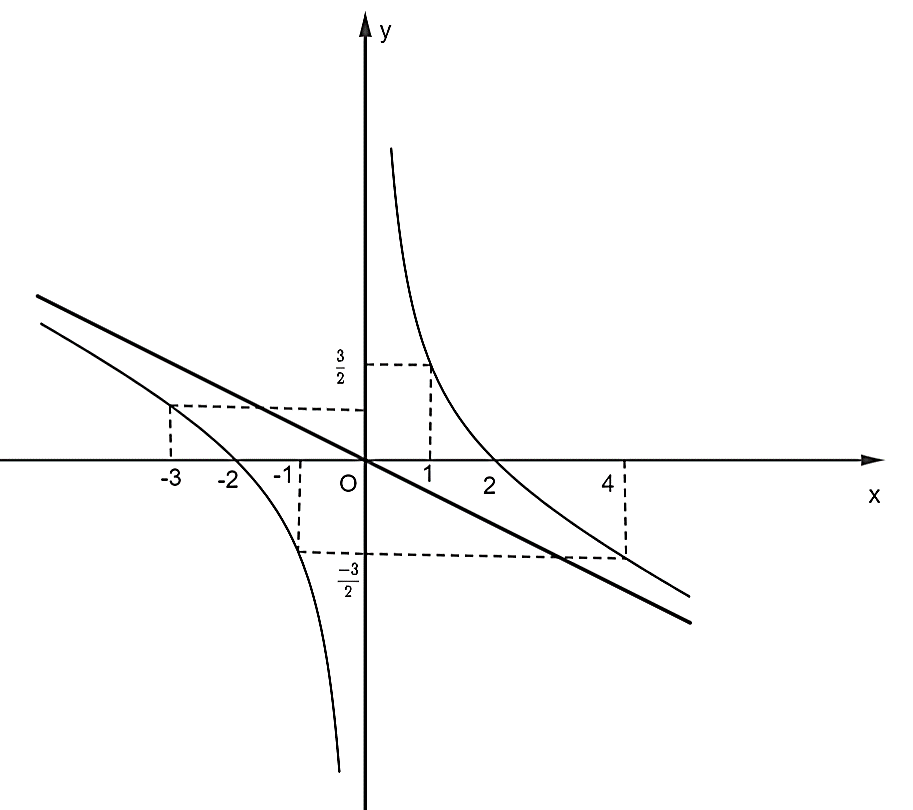
Đồ thị hàm số nhận giao điểm của hai đường tiệm cận có tọa độ (0; 0) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272