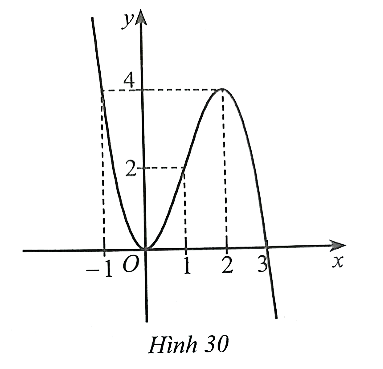
Cho hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d có đồ thị là đường cong như Hình 30.
|
a) Phương trình f(x) = 4 có hai nghiệm x = −1, x = 2. |
Đ |
S |
|
b) Phương trình f(x) = −1 có hai nghiệm. |
Đ |
S |
|
c) Phương trình f(x) = 2 có ba nghiệm. |
Đ |
S |
|
d) Phương trình f(f(x)) = 4 có sáu nghiệm. |
Đ |
S |
Quảng cáo
1 câu trả lời 138
|
a) Đ |
b) S |
c) Đ |
d) S |
Dựa vào đồ thị hàm số Hình 30, ta có:
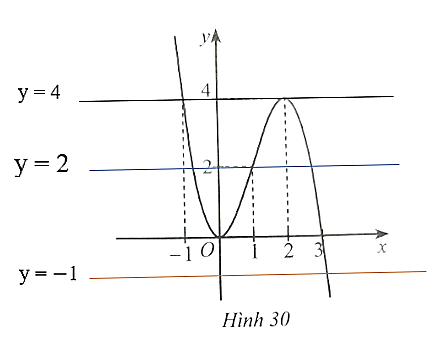
Đường thẳng y = 4 cắt đồ thị hàm số y = f(x) tại hai điểm có hoành độ bằng −1 và 2 nên phương trình f(x) = 4 có hai nghiệm phân biệt là x = −1 và x = 2.
Đường thẳng y = −1 cắt đồ thị hàm số y = f(x) tại một điểm nên phương trình f(x) = −1 có một nghiệm.
Đường thẳng y = 2 cắt đồ thị hàm số y = f(x) tại ba điểm nên phương trình f(x) = 2 có ba nghiệm.
Ta có: f(f(x)) = 4 khi f(x) = 2 hoặc f(x) = −1.
Với f(x) = −1, phương trình có một nghiệm.
Với f(x) = 2 phương trình có ba nghiệm.
Vậy f(f(x)) = 4 có 4 nghiệm.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129621
Đã trả lời bởi chuyên gia
129621 -
 Đã trả lời bởi chuyên gia
104033
Đã trả lời bởi chuyên gia
104033 -
 Đã trả lời bởi chuyên gia
94043
Đã trả lời bởi chuyên gia
94043 -
 Đã trả lời bởi chuyên gia
69192
Đã trả lời bởi chuyên gia
69192



