Cho hàm số y = 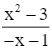 .
.
|
a) Đồ thị hàm số có tiệm cận đứng là đường thẳng x = −1. |
Đ |
S |
|
b) Đồ thị hàm số có tiệm cận ngang là đường thẳng y = −1. |
Đ |
S |
|
c) Đồ thị hàm số có tiệm cận xiên là đường thẳng y = −x. |
Đ |
S |
|
d) Giao điểm I của hai đường tiệm cận của đồ thị hàm số là I(−1; 1). |
Đ |
S |
Quảng cáo
1 câu trả lời 90
|
a) Đ |
b) S |
c) S |
d) S |
Ta có: y = 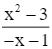 .
.
Tập xác định: D = ℝ\{−1}.
Ta có: ![]() y =
y = ![]()
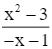 = −∞,
= −∞, ![]() y =
y = ![]()
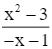 = +∞.
= +∞.
Do đó, đường thẳng x = −1 là tiệm cận đứng của đồ thị hàm số đã cho.
Ta có: ![]() y =
y = ![]()
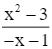 = +∞ ,
= +∞ , ![]() y =
y = ![]()
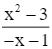 = −∞.
= −∞.
Do đó, đồ thị hàm số không có tiệm cận ngang.
Ta có: ![]() [y – (– x)] =
[y – (– x)] = ![]()
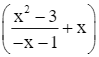 =
=![]()
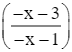 = 1 ≠ 0.
= 1 ≠ 0.
![]() [y – (– x)] =
[y – (– x)] = ![]()
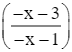 = 1 ≠ 0.
= 1 ≠ 0.
Do đó, đồ thị hàm số không có tiệm cận xiên.
Do đồ thị hàm số chỉ có 1 đường điệm cận nên không tồn tại giao điểm I của hai đường tiệm cận.
Quảng cáo
Bạn muốn hỏi bài tập?



