Bác Lâm muốn gò một cái thùng bằng tôn dạng hình hộp chữ nhật không nắp có đáy là hình vuông và đựng đầy được 32 lít nước. Gọi độ dài cạnh đáy của thùng là x (dm), chiều cao của thùng là h (dm).
|
a) Thể tích của thùng V = x2. h (dm3). |
Đ |
S |
|
b) Tổng diện tích xung quanh và diện tích đáy của thùng là: S = 4xh + x2 (dm2). |
Đ |
S |
|
c) Đạo hàm của hàm số S(x) = |
Đ |
S |
|
d) Để làm được thùng mà tốn ít nguyên liệu nhất thì độ dài cạnh đáy của thùng là 4 dm. |
Đ |
S |
Quảng cáo
1 câu trả lời 462
|
a) Đ |
b) Đ |
c) S |
d) Đ |
Thể tích của thùng chính bằng thể tích hình hộp nên V = x2. h (dm3).
Tổng diện tích xung quanh và diện tích 1 đáy của thùng (do thùng không nắp) là:
S = 4xh + x2 (dm2).
Theo đề, cái gò đựng đầy được 32 lít nước, tức là V = 32 (dm3).
⇒ x2. h = 32 ⇒ h = ![]() .
.
Khi đó S(x) = 4x.![]() + x2 =
+ x2 = ![]() .
.
Ta có: S(x) = ![]() ⇒ S'(x) =
⇒ S'(x) = ![]()
S'(x) = 0 ⇔ ![]() = 0 ⇔ x = 4.
= 0 ⇔ x = 4.
Ta có bảng biến thiên như sau:
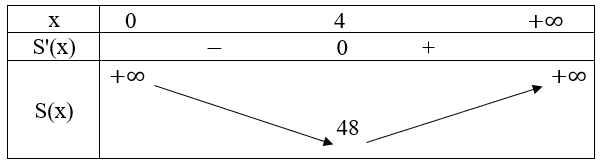
Vậy để làm được thùng mà tốn ít nguyên liệu nhất thì độ dài cạnh đáy của thùng là
4 dm.
Quảng cáo
Bạn muốn hỏi bài tập?



