Quảng cáo
5 câu trả lời 761
Để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( f(x) = \frac{x}{4} + x^2 \) trên tập số thực \( \mathbb{R} \), chúng ta cần thực hiện các bước sau:
### Bước 1: Tính đạo hàm của hàm số
Tính đạo hàm của hàm số \( f(x) \):
\[
f(x) = \frac{x}{4} + x^2
\]
\[
f'(x) = \frac{d}{dx}\left(\frac{x}{4}\right) + \frac{d}{dx}(x^2)
\]
\[
f'(x) = \frac{1}{4} + 2x
\]
### Bước 2: Tìm điểm cực trị
Để tìm các điểm cực trị, chúng ta giải phương trình đạo hàm bằng 0:
\[
f'(x) = \frac{1}{4} + 2x = 0
\]
\[
2x = -\frac{1}{4}
\]
\[
x = -\frac{1}{8}
\]
### Bước 3: Tính giá trị của hàm số tại điểm cực trị
Thay \( x = -\frac{1}{8} \) vào hàm số \( f(x) \):
\[
f\left(-\frac{1}{8}\right) = \frac{-\frac{1}{8}}{4} + \left(-\frac{1}{8}\right)^2
\]
\[
= -\frac{1}{32} + \frac{1}{64}
\]
\[
= -\frac{2}{64} + \frac{1}{64}
\]
\[
= -\frac{1}{64}
\]
### Bước 4: Xác định giá trị lớn nhất và giá trị nhỏ nhất
- Hàm số \( f(x) = \frac{x}{4} + x^2 \) là một hàm bậc hai với hệ số \( x^2 \) dương, do đó, hàm số có giá trị nhỏ nhất tại điểm cực trị và tiến ra vô cực khi \( x \) tiến ra vô cực.
- **Giá trị nhỏ nhất** của hàm số là:
\[
f\left(-\frac{1}{8}\right) = -\frac{1}{64}
\]
- **Giá trị lớn nhất** không tồn tại, vì hàm số tiến ra vô cực khi \( x \) tiến ra vô cực.
**Tóm tắt:**
- **Giá trị nhỏ nhất** của hàm số \( f(x) = \frac{x}{4} + x^2 \) là \( -\frac{1}{64} \).
- **Giá trị lớn nhất** không tồn tại (hàm số có giá trị lớn nhất không bị giới hạn trên \( \mathbb{R} \)).
Để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( f(x) = \frac{x}{4} + x^2 \) trên \( \mathbb{R} \), ta thực hiện các bước sau:
1. **Tính đạo hàm của hàm số** \( f(x) \) để tìm các điểm cực trị:
\[
f'(x) = \frac{1}{4} + 2x
\]
2. **Giải phương trình** \( f'(x) = 0 \) để tìm các điểm cực trị:
\[
\frac{1}{4} + 2x = 0
\]
\[
2x = -\frac{1}{4}
\]
\[
x = -\frac{1}{8}
\]
3. **Xét dấu của đạo hàm** \( f'(x) \) để xác định tính chất của điểm cực trị:
- Khi \( x < -\frac{1}{8} \), \( f'(x) < 0 \) (hàm số giảm).
- Khi \( x > -\frac{1}{8} \), \( f'(x) > 0 \) (hàm số tăng).
Điều này có nghĩa là tại \( x = -\frac{1}{8} \), hàm số đạt giá trị nhỏ nhất.
4. **Tính giá trị nhỏ nhất**:
\[
f\left(-\frac{1}{8}\right) = \frac{-\frac{1}{8}}{4} + \left(-\frac{1}{8}\right)^2 = -\frac{1}{32} + \frac{1}{64} = -\frac{1}{64}
\]
5. **Xét giới hạn của hàm số khi \( x \to \pm\infty \)**:
- Khi \( x \to \infty \) hoặc \( x \to -\infty \), \( f(x) \to \infty \).
Vậy giá trị lớn nhất của hàm số không tồn tại (hàm số tăng không giới hạn), và giá trị nhỏ nhất của hàm số là \( -\frac{1}{64} \) tại \( x = -\frac{1}{8} \).
Để tìm giá trị lớn nhất và nhỏ nhất của hàm số f(x)=x4+x2f(x) = \frac{x}{4} + x^2f(x)=4x+x2 trên tập số thực R\mathbb{R}R, ta thực hiện các bước sau:
1. Xét hàm số:
f(x)=x4+x2f(x) = \frac{x}{4} + x^2f(x)=4x+x22. Tính đạo hàm của hàm số:
f′(x)=14+2xf'(x) = \frac{1}{4} + 2xf′(x)=41+2x3. Tìm các điểm mà tại đó f′(x)=0f'(x) = 0f′(x)=0:
14+2x=0\frac{1}{4} + 2x = 041+2x=0 2x=−142x = -\frac{1}{4}2x=−41 x=−18x = -\frac{1}{8}x=−814. Xét dấu đạo hàm để tìm giá trị lớn nhất và nhỏ nhất:
Xét đạo hàm tại x=−18x = -\frac{1}{8}x=−81:
f′(−18)=0f'(-\frac{1}{8}) = 0f′(−81)=0 nên đây là điểm cực trị.
Tính giá trị của hàm số tại x=−18x = -\frac{1}{8}x=−81:
f(−18)=−184+(−18)2=−132+164=−164f\left(-\frac{1}{8}\right) = \frac{-\frac{1}{8}}{4} + \left(-\frac{1}{8}\right)^2 = -\frac{1}{32} + \frac{1}{64} = -\frac{1}{64}f(−81)=4−81+(−81)2=−321+641=−641Vậy, tại x=−18x = -\frac{1}{8}x=−81, hàm số đạt giá trị nhỏ nhất là −164-\frac{1}{64}−641.
5. Xét giới hạn của hàm số khi x→±∞x \to \pm \inftyx→±∞:
limx→±∞(x4+x2)=∞\lim_{x \to \pm \infty} \left( \frac{x}{4} + x^2 \right) = \inftyx→±∞lim(4x+x2)=∞Điều này cho thấy hàm số không có giá trị lớn nhất trên R\mathbb{R}R vì nó có thể tăng vô hạn.
Kết luận:
Giá trị nhỏ nhất của hàm số là −164-\frac{1}{64}−641 tại x=−18x = -\frac{1}{8}x=−81.
Hàm số không có giá trị lớn nhất trên R\mathbb{R}R.

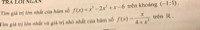
Quảng cáo
Bạn muốn hỏi bài tập?


