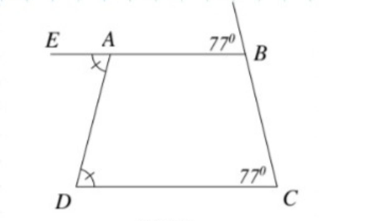
Để chứng minh các kết luận liên quan đến hình học, trước tiên ta cần biết cấu trúc của hình 9 và các yếu tố liên quan như các đoạn thẳng, góc, và các đường thẳng. Do đó, tôi sẽ giải thích cách chứng minh các điều này dựa trên các giả thiết thông thường của hình học. Nếu bạn có một hình vẽ cụ thể, hãy cung cấp thêm thông tin chi tiết để tôi có thể hỗ trợ chính xác hơn.

Dưới đây là các phương pháp chứng minh thường gặp cho các loại câu hỏi này:

### a) Chứng tỏ rằng \( AE \parallel DC \)

Để chứng minh \( AE \parallel DC \), ta có thể sử dụng định lý về góc đồng vị, góc so le trong hoặc góc trong cùng phía tùy thuộc vào hình của bạn. Dưới đây là một cách thường dùng để chứng minh hai đoạn thẳng song song:

**Giả sử:**

- Hình của bạn có thể là một hình thang hoặc một hình với hai đường chéo cắt nhau.
- Ta cần chứng minh rằng các góc tạo thành với các đường chéo hoặc các góc ngoài liên quan là đồng vị hoặc so le trong.

**Phương pháp chứng minh:**

1. **Sử dụng góc đồng vị hoặc góc so le trong:**
- Nếu trong hình có một đường thẳng cắt hai đường song song \( AE \) và \( DC \), thì các góc đồng vị hoặc góc so le trong liên quan đến các đoạn thẳng này sẽ bằng nhau.
- Ví dụ: Nếu \( \angle AEB \) và \( \angle DCF \) là các góc đồng vị hoặc góc so le trong, và chúng bằng nhau, thì \( AE \parallel DC \).

2. **Sử dụng định lý về hai đường chéo cắt nhau:**
- Nếu \( AE \) và \( DC \) là các cạnh của một hình thang hoặc hình với hai đường chéo, hãy kiểm tra xem các góc ngoài hoặc các góc phụ thuộc có bằng nhau hay không.

### b) Chứng tỏ rằng \( BA \parallel DC \)

Để chứng minh \( BA \parallel DC \), ta có thể sử dụng cách tương tự như trên hoặc dựa vào hình học của tam giác hoặc hình thang.

**Phương pháp chứng minh:**

1. **Sử dụng định lý góc trong:**
- Nếu \( BA \) là một đường cắt hai đường \( DC \) và một đoạn thẳng khác tạo thành các góc đồng vị hoặc góc so le trong với \( DC \), và các góc này bằng nhau, thì \( BA \parallel DC \).

2. **Sử dụng định lý về đường chéo:**
- Nếu \( BA \) và \( DC \) là các cạnh của một hình thang hoặc hình có hai đường chéo, kiểm tra xem các góc phụ thuộc vào các đoạn thẳng này có bằng nhau hay không.

### c) Chứng tỏ rằng ba điểm \( E, A, B \) thẳng hàng

Để chứng minh ba điểm \( E, A, B \) thẳng hàng, ta cần chứng minh rằng các điểm này nằm trên một đường thẳng duy nhất.

**Phương pháp chứng minh:**

1. **Sử dụng các đoạn thẳng hoặc góc:**
- Nếu ta biết rằng \( E \) và \( A \) nằm trên một đường thẳng, và \( A \) và \( B \) cũng nằm trên một đường thẳng, thì \( E, A, B \) sẽ thẳng hàng.

2. **Sử dụng các định lý về đường chéo và các góc:**
- Nếu \( E \) và \( A \) cùng nằm trên một đoạn thẳng và \( B \) là một điểm trên đoạn thẳng đó, thì \( E, A, B \) sẽ thẳng hàng.

Nếu bạn có một hình vẽ cụ thể hoặc thêm thông tin về hình học của bài toán, tôi có thể cung cấp các chứng minh cụ thể hơn dựa trên thông tin đó.