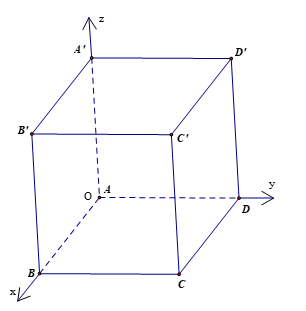
Chọn hệ trục tọa độ như hình vẽ với O trùng với A.

Ta có A'(0; 0; 3), B(1; 0; 0), A(0; 0; 0), C(1; 5; 0), B'(1; 0; 3), D(0; 5; 0), C'(1; 5; 3)

a) Đường thẳng AC nhận \(\overrightarrow {AC} = \left( {1;5;0} \right)\) làm vectơ chỉ phương.

Đường thẳng BA' nhận \(\overrightarrow {BA'} = \left( { - 1;0;3} \right)\) làm vectơ chỉ phương.

Khi đó \(\cos \left( {AC,BA'} \right) = \frac{{\left| {1.\left( { - 1} \right) + 5.0 + 0.3} \right|}}{{\sqrt {{1^2} + {5^2}} .\sqrt {{{\left( { - 1} \right)}^2} + {3^2}} }} = \frac{1}{{2\sqrt {65} }}\).

Suy ra (AC, BA') ≈ 86,44°.

b) Ta có \(\overrightarrow {BB'} = \left( {0;0;3} \right),\overrightarrow {BD} = \left( { - 1;5;0} \right)\), \(\overrightarrow {AC} = \left( {1;5;0} \right)\), \(\overrightarrow {AA'} = \left( {0;0;3} \right)\).

Ta có \(\left[ {\overrightarrow {BB'} ,\overrightarrow {BD} } \right] = \left( { - 15; - 3;0} \right)\), \(\left[ {\overrightarrow {AC} ,\overrightarrow {AA'} } \right] = \left( {15; - 3;0} \right)\).

Mặt phẳng (BB'D'D) nhận \(\overrightarrow n = - \frac{1}{3}\left[ {\overrightarrow {BB'} ,\overrightarrow {BD} } \right] = \left( {5;1;0} \right)\) làm vectơ pháp tuyến.

Mặt phẳng (AA'C'C) nhận \(\overrightarrow {n'} = \frac{1}{3}\left[ {\overrightarrow {AC} ,\overrightarrow {AA'} } \right] = \left( {5; - 1;0} \right)\) làm vectơ pháp tuyến.

Khi đó \(\cos \left( {\left( {BB'D'D} \right),\left( {AA'C'C} \right)} \right) = \frac{{\left| {5.5 + 1.\left( { - 1} \right) + 0.0} \right|}}{{\sqrt {{5^2} + 1} .\sqrt {{5^2} + 1} }} = \frac{{24}}{{26}} = \frac{{12}}{{13}}\).

Suy ra ((BB'D'D), (AA'C'C)) ≈ 22,62°.

c) Ta có \(\overrightarrow {AC'} = \left( {1;5;3} \right)\), \(\overrightarrow {A'B} = \left( {1;0; - 3} \right),\overrightarrow {A'D} = \left( {0;5; - 3} \right)\), \(\left[ {\overrightarrow {A'B} ,\overrightarrow {A'D} } \right] = \left( {15;3;5} \right)\).

Đường thẳng AC' nhận \(\overrightarrow {AC'} = \left( {1;5;3} \right)\) làm vectơ chỉ phương.

Mặt phẳng (A'BD) nhận \(\overrightarrow n = \left[ {\overrightarrow {A'B} ,\overrightarrow {A'D} } \right] = \left( {15;3;5} \right)\) làm vectơ pháp tuyến.

Ta có \(\sin \left( {AC',\left( {A'BD} \right)} \right) = \frac{{\left| {1.15 + 5.3 + 3.5} \right|}}{{\sqrt {{1^2} + {5^2} + {3^2}} .\sqrt {{{15}^2} + {3^2} + {5^2}} }} = \frac{{45}}{{7\sqrt {185} }}\).

Suy ra (AC', (A'BD)) ≈ 28,21°.