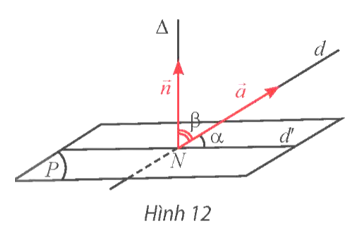
Cho đường thẳng d có vectơ chỉ phương \(\overrightarrow a = \left( {{a_1};{a_2};{a_3}} \right)\) và mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n = \left( {{n_1};{n_2};{n_3}} \right)\). Biết d cắt (P) tại điểm N và hình chiếu vuông góc của d lên (P) là đường thẳng d'. Qua N vẽ đường thẳng D vuông góc với (P) (Hình 12).
a) Nhắc lại định nghĩa góc giữa đường thẳng và mặt phẳng trong không gian.
b) Có nhận xét gì về số đo của hai góc α = (d, d'); β = (D, d)?
c) Giải thích tại sao ta lại có đẳng thức: \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\overrightarrow a ,\overrightarrow n } \right)} \right|\).
Quảng cáo
1 câu trả lời 66
a) Nếu đường thẳng a không vuông góc với (P) thì góc giữa a và hình chiếu a' của a trên (P) gọi là góc giữa đường thẳng a và (P). Kí hiệu (a, (P)).
b) Ta có α + β = 90° hay (d, d') + (D, d) = 90° Þ (d, d') = 90° − (D, d).
c) Vì (d, (P)) = (d, d') = 90° − (D, d).
Do đó sin(d, (P)) = sin(90° − (D, d)) = cos(D, d) = \(\left| {\cos \left( {\overrightarrow a ,\overrightarrow n } \right)} \right|\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272



