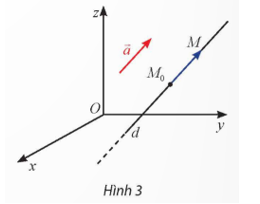
Trong không gian Oxyz, cho đường thẳng d đi qua điểm M0(x0; y0; z0) cố định và có vectơ chỉ phương là \(\overrightarrow a = \left( {{a_1};{a_2};{a_3}} \right)\) khác \(\overrightarrow 0 \).
a) Giải thích tại sao ta có thể viết: M Î d Û \(\overrightarrow {{M_0}M} = t\overrightarrow a ,\left( {t \in \mathbb{R}} \right)\).
b) Với M(x; y; z) thuộc d, hãy tính x, y, z theo x0, y0, z0 và a1, a2, a3.
Quảng cáo
1 câu trả lời 58
a) Ta có M Î d thì \(\overrightarrow {{M_0}M} \) cùng phương với \(\overrightarrow a \). Do đó \(\overrightarrow {{M_0}M} = t\overrightarrow a ,\left( {t \in \mathbb{R}} \right)\).
b) Ta có \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\).
Mà \(\overrightarrow {{M_0}M} = t\overrightarrow a \) nên \(\left\{ \begin{array}{l}x - {x_0} = {a_1}t\\y - {y_0} = {a_2}t\\z - {z_0} = {a_3}t\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_3}t\end{array} \right.,t \in \mathbb{R}\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272



