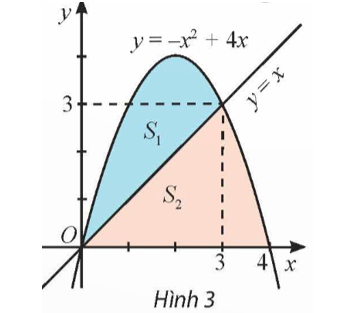
Cho S1, S2 là diện tích các hình phẳng được mô tả trong Hình 3. Tính .
Quảng cáo
1 câu trả lời 103
Ta có \({S_1} = \int\limits_0^3 {\left| { - {x^2} + 4x - x} \right|dx} \)\( = \int\limits_0^3 {\left| { - {x^2} + 3x} \right|dx} \)\( = \int\limits_0^3 {\left( { - {x^2} + 3x} \right)dx} \)\( = \left. {\left( { - \frac{{{x^3}}}{3} + \frac{{3{x^2}}}{2}} \right)} \right|_0^3\)\( = \frac{9}{2}\).
\({S_2} = \int\limits_0^3 {\left| x \right|} dx + \int\limits_3^4 {\left| { - {x^2} + 4x} \right|dx} \)\( = \int\limits_0^3 x dx + \int\limits_3^4 {\left( { - {x^2} + 4x} \right)dx} \)
\( = \left. {\frac{{{x^2}}}{2}} \right|_0^3 + \left. {\left( { - \frac{{{x^3}}}{3} + 2{x^2}} \right)} \right|_3^4\)\( = \frac{9}{2} + \frac{{32}}{3} - 9 = \frac{{37}}{6}\).
Do đó \(\frac{{{S_1}}}{{{S_2}}} = \frac{9}{2}:\frac{{37}}{6} = \frac{{27}}{{37}}\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272



