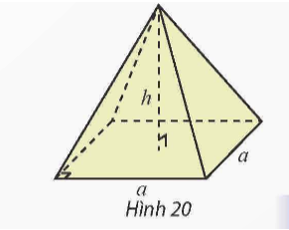
Sử dụng tích phân, tính thể tích của hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng h (Hình 20).
Quảng cáo
1 câu trả lời 152
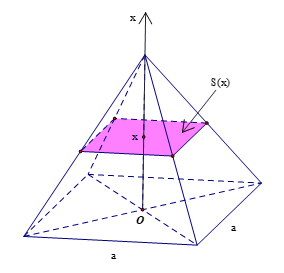
Chọn trục Ox trùng với đường cao của hình chóp đều như hình vẽ, sao cho mặt đáy nằm trong mặt phẳng vuông góc với trục Ox tại x = 0.
Mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ h) cắt hình chóp đều theo mặt cắt là hình vuông đồng dạng với đáy của hình chóp theo tỉ số \(\frac{x}{h}\).
Do đó \(\frac{{S\left( x \right)}}{{{a^2}}} = {\left( {\frac{x}{h}} \right)^2}\)\( \Rightarrow S\left( x \right) = {\left( {\frac{x}{h}} \right)^2}{a^2} = \frac{{{a^2}}}{{{h^2}}}{x^2}\).
Do đó thể tích khối chóp tứ giác đều là:
\(V = \int\limits_0^h {\frac{{{a^2}}}{{{h^2}}}{x^2}dx} \)\( = \left. {\left( {\frac{{{a^2}}}{{{h^2}}}.\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{1}{3}{a^2}h\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272



