Trong không gian với hệ trục toạ độ Oxyz, cho hình lập phương OBCD.O'B'C'D' có O(0; 0; 0), B(a; 0; 0), D(0; a; 0), O'(0; 0; a) với a > 0.
Quảng cáo
1 câu trả lời 85
Gọi tọa độ điểm C là C(xC; yC; zC). Ta có ![]() .
.
Vì OBCD.O'B'C'D' là hình lập phương nên OBCD là hình vuông, do đó ta có
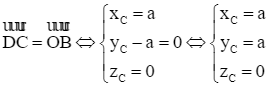 .
.
Suy ra C(a; a; 0).
Gọi tọa độ điểm B' là B'(xB'; yB'; zB'). Ta có ![]() .
.
Ta có 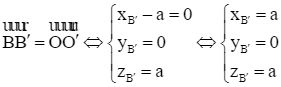 . Suy ra B'(a; 0; a).
. Suy ra B'(a; 0; a).
Gọi tọa độ điểm D' là D'(xD'; yD'; zD'). Khi đó ![]() .
.
Ta có 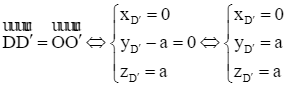 . Suy ra D'(0; a; a).
. Suy ra D'(0; a; a).
Ta có ![]() .
.
Xét vectơ 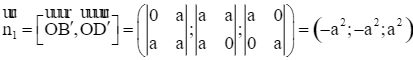 .
.
Khi đó ![]() là một vectơ pháp tuyến của mặt phẳng (OB'D').
là một vectơ pháp tuyến của mặt phẳng (OB'D').
Lại có ![]() . Ta có
. Ta có ![]() , suy ra hai vectơ
, suy ra hai vectơ ![]() cùng phương.
cùng phương.
Do đó, ![]() cũng là một vectơ pháp tuyến của mặt phẳng (OB'D').
cũng là một vectơ pháp tuyến của mặt phẳng (OB'D').
Vậy đường chéo O'C vuông góc với mặt phẳng (OB'D').
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272



