Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biết cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.
So sánh: P(A ∩ B) và P(B) ∙ P(A | B);
P() và P() ∙ P(A | ).
Từ đó, hãy chứng tỏ rằng: P(A) = P(B) ∙ P(A | B) + P() ∙ P(A | ).
Quảng cáo
1 câu trả lời 93
1 năm trước
Ta có P(B) ∙ P(A | B) = P(B) ∙ 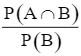 = P(A ∩ B).
= P(A ∩ B).
P(![]() ) ∙ P(A |
) ∙ P(A | ![]() ) = P(
) = P(![]() ) ∙
) ∙ 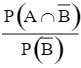 = P(
= P(![]() ).
).
Vì hai biến cố A ∩ B và ![]() là hai biến cố xung khắc và (A ∩ B) ∪ (
là hai biến cố xung khắc và (A ∩ B) ∪ (![]() ) = A nên theo công thức xác suất ta có
) = A nên theo công thức xác suất ta có
P(A) = P(A ∩ B) + P(![]() ) = P(B) ∙ P(A | B) + P(
) = P(B) ∙ P(A | B) + P(![]() ) ∙ P(A |
) ∙ P(A | ![]() ).
).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272
Gửi báo cáo thành công!



