Giải bài toán quy hoạch tuyến tính:
F = 10x + 20y → min
với ràng buộc
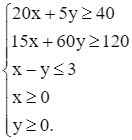
Quảng cáo
1 câu trả lời 183
Viết lại ràng buộc của bài toán thành 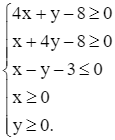
Tập phương án Ω của bài toán là miền không gạch chéo trên hình dưới đây (không là miền đa giác).
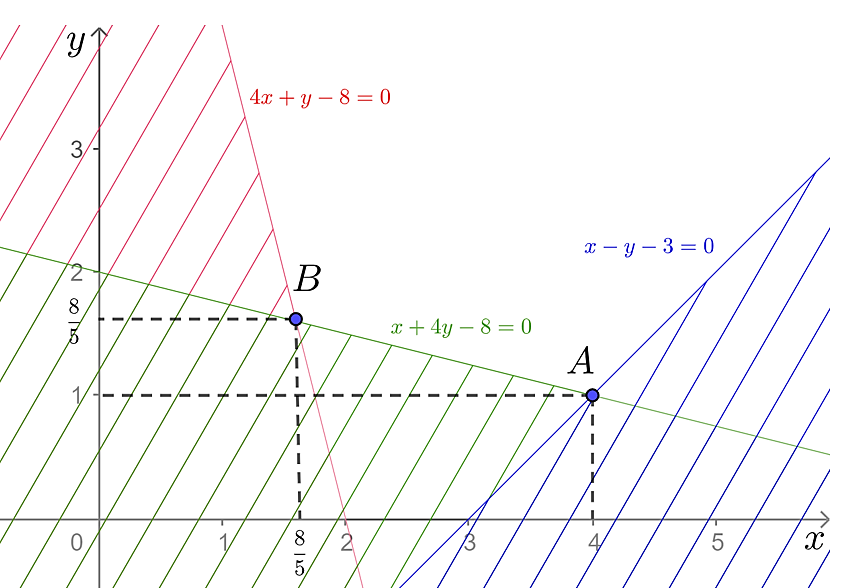
Tọa độ điểm A là nghiệm của hệ
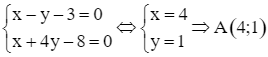 .
.
Tương tự, tìm được 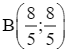 .
.
Miền Ω có hai đỉnh là A(4; 1) và 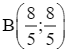 .
.
Do Ω nằm trong góc phần tư thứ nhất và các hệ số của biểu thức F = 10x + 20y đều dương nên F đạt giá trị nhỏ nhất tại một đỉnh của Ω.
Ta có F(4; 1) = 10 ∙ 4 + 20 ∙ 1 = 60; 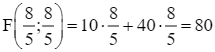 .
.
Vậy F đạt giá trị nhỏ nhất tại đỉnh A(4; 1) và ![]() .
.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272
Gửi báo cáo thành công!



