Ta giải bài toán Tình huống mở đầu.
Từ HĐ1 ta có bài toán quy hoạch tuyến tính sau:
F(x; y) = 40x + 30y → max
Với các ràng buộc
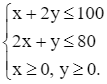
Miền chấp nhận được S của bài toán là miền tứ giác tô màu trong Hình 2.3.
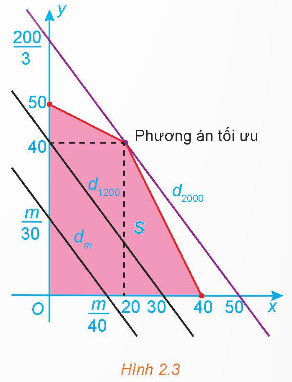
Với mỗi số thực m xét đường thẳng dm: 40x + 30y = m.
Từ hình vẽ, tìm điều kiện của m để dm ∩ S ≠ ∅.
Quảng cáo
1 câu trả lời 58
Đường thẳng dm song song với AB, có phương không đổi, do đó từ hình vẽ, ta thấy đường thẳng dm: 40x + 30y = m luôn cắt trục tung tại điểm có tung độ 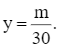
Từ hình vẽ, ta thấy rằng để dm ∩ S ≠ ∅ thì 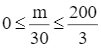 tức là 0 ≤ m ≤ 2 000.
tức là 0 ≤ m ≤ 2 000.
Vậy 0 ≤ m ≤ 2 000.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272
Gửi báo cáo thành công!



