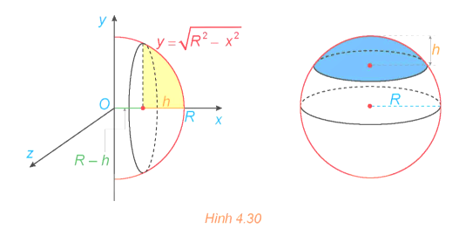
Khối chỏm cầu có bán kính R và chiều cao h (0 < h ≤ R) sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình , trục hoành và hai đường thẳng x = R – h, x = R xung quanh trục Ox (H.4.30). Tính thể tích của khối chỏm cầu này.
Quảng cáo
1 câu trả lời 116
Thể tích cần tìm là:
\(V = \pi \int\limits_{R - h}^R {\left( {{R^2} - {x^2}} \right)dx} \)\( = \pi \left. {\left( {{R^2}x - \frac{{{x^3}}}{3}} \right)} \right|_{R - h}^R\)
\( = \pi \left( {{R^3} - \frac{{{R^3}}}{3} - {R^2}\left( {R - h} \right) + \frac{{{{\left( {R - h} \right)}^3}}}{3}} \right)\)\( = \pi \left( {{R^3} - \frac{{{R^3}}}{3} - {R^3} + {R^2}h + \frac{{{R^3}}}{3} - {R^2}h + R{h^2} - \frac{{{h^3}}}{3}} \right)\)
\( = \pi \left( {R{h^2} - \frac{{{h^3}}}{3}} \right)\)\( = \pi {h^2}\left( {R - \frac{h}{3}} \right)\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129637
Đã trả lời bởi chuyên gia
129637 -
 Đã trả lời bởi chuyên gia
104061
Đã trả lời bởi chuyên gia
104061 -
 Đã trả lời bởi chuyên gia
94054
Đã trả lời bởi chuyên gia
94054 -
 Đã trả lời bởi chuyên gia
69272
Đã trả lời bởi chuyên gia
69272



